题目内容
若Z=
(i为虚数单位),则Z的共轭复数为( )
| 2-i |
| 1+i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:由复数代数形式的除法运算化简复数z,则z的共轭复数可求.
解答:
解:∵z=
=
=
=
-
i,
∴z的共轭复数为:
+
i.
故选:A.
| 2-i |
| 1+i |
| (2-i)(1-i) |
| (1+i)(1-i) |
| 1-3i |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴z的共轭复数为:
| 1 |
| 2 |
| 3 |
| 2 |
故选:A.
点评:本题考查了复数代数形式的除法运算,考查了共轭复数的求法,是基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
|
|=1,|
|=2,
=
+
,
⊥
,则
与
的夹角等于( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、90° |
定义行列式运算
=a1a4-a2a3,将函数f(x)=
的图象向右平移m(m>0)个单位,所得图象对应的函数为奇函数,则m的最小值为( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
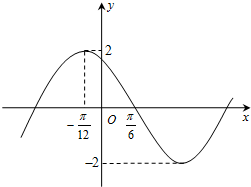 已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )
已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(6x-
| ||
D、f(x)=2sin(6x+
|
在平面直角坐标系中,记抛物线y=x-x2与x轴所围成的平面区域为M,该抛物线与直线y=kx(k>0)所围成的平面区域为A,向区域M内随机抛掷一点P,若点P落在区域A内的概率为
,则k的值为( )
| 8 |
| 27 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,则f(2014)=( )
|
| A、2014 | ||
B、
| ||
| C、2015 | ||
D、
|
已知i为虚数单位,a∈R,如果复数2i-
是实数,则a的值为( )
| a |
| 1-i |
| A、-4 | B、2 | C、-2 | D、4 |