题目内容
定义行列式运算
=a1a4-a2a3,将函数f(x)=
的图象向右平移m(m>0)个单位,所得图象对应的函数为奇函数,则m的最小值为( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由定义的行列式运算得到函数f(x),化简后利用函数图象的平移得到g(x)=2cos(2x+
-2m),再由该函数为奇函数得到m=-
π-
,k∈Z,由此求得最小正数m的值.
| π |
| 6 |
| k |
| 2 |
| π |
| 6 |
解答:
解:由定义行列式运算
=a1a4-a2a3,得
f(x)=
=
cos2x-sin2x
=2(
cos2x-
sin2x)
=2cos(2x+
).
将函数f(x)的图象向右平移m(m>0)个单位,所得图象对应的函数解析式为:
g(x)=f(x-m)=2cos[2(x-m)+
]=2cos(2x+
-2m),
∵函数g(x)为奇函数,
∴
-2m=kπ+
,k∈Z,
即m=-
π-
,k∈Z,
取k=-1时,正数m的最小值为
.
故选:C.
|
f(x)=
|
| 3 |
=2(
| ||
| 2 |
| 1 |
| 2 |
=2cos(2x+
| π |
| 6 |
将函数f(x)的图象向右平移m(m>0)个单位,所得图象对应的函数解析式为:
g(x)=f(x-m)=2cos[2(x-m)+
| π |
| 6 |
| π |
| 6 |
∵函数g(x)为奇函数,
∴
| π |
| 6 |
| π |
| 2 |
即m=-
| k |
| 2 |
| π |
| 6 |
取k=-1时,正数m的最小值为
| π |
| 3 |
故选:C.
点评:本题考查了三角函数的图象和性质,考查了三角函数的图象平移问题,训练了三角函数为奇函数的条件,是中档题.

练习册系列答案
相关题目
2014年3月,为了调查教师对第十二届全国人民代表大会二次会议的了解程度,安庆市拟采用分层抽样的方法从A,B,C三所不同的中学抽取60名教师进行调查.已知A,B,C学校中分别有180,270,90名教师,则从C学校中应抽取的人数为( )
| A、10 | B、12 | C、18 | D、24 |
(理)不等式4x2-7x-2<0成立的一个必要不充分条件是( )
A、(-
| ||
B、(-∞,-
| ||
C、(-
| ||
| D、(-1,2) |
若集合A={x||x|+x>0},B={x|x2-5x+6≥0},则A∩B=( )
| A、{x|2≤x≤3} |
| B、{x|0≤x≤2或x≥3} |
| C、{x|0<x≤2或x≥3} |
| D、{x|x≥3} |
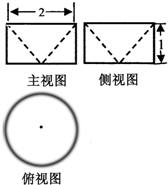 已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )
已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )| A、1:4 | B、1:2 |
| C、1:1 | D、2:1 |
执行如图所示的程序框图,输出的S值为( )


| A、2 | B、-2 | C、4 | D、-4 |
若Z=
(i为虚数单位),则Z的共轭复数为( )
| 2-i |
| 1+i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|