Question

在平面直角坐标系中，记抛物线y=x-x²与x轴所围成的平面区域为M，该抛物线与直线y=kx（k＞0）所围成的平面区域为A，向区域M内随机抛掷一点P，若点P落在区域A内的概率为

8

27

，则k的值为（　　）

• A、

  1

  3

• B、

  2

  3

• C、

  1

  2

• D、

  3

  4

Answer 1

考点：几何概型

专题：导数的综合应用,概率与统计

分析：根据定积分的几何意义，利用定积分计算公式算出抛物线y=x-x²与x轴所围成的平面区域M的面积S=

1

6

，从而由几何概型公式算出抛物线与y=kx围成的平面区域A的面积为S'=

4

81

．由此算出y=x-x²与y=kx在第一象限的交点坐标，利用定积分公式建立关于k的方程，解之即可得到实数k的值．

解答： 解：∵抛物线y=x-x²与x轴交于点（0，0）与（1，0），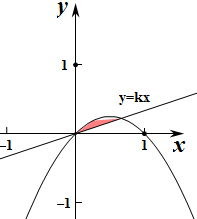
∴根据定积分的几何意义，可得抛物线与x轴所围成的平面区域M的面积为
S=

∫

1 0

（x-x²）dx=（

1

2

x2-

1

3

x3）|

1 0

=

1

6

．
设抛物线与直线y=kx（k＞0）所围成的平面区域A的面积为S'，
∵向区域M内随机抛掷一点P，点P落在区域A内的概率为

8

27

，
∴

S′

S

=

8

27

，可得S'=

8

27

S=

4

81

，
求出y=x-x²与y=kx的交点中，除原点外的点B坐标为（1-k，k-k²），
可得S'=

∫

1-k 0

[（x-x²）-kx]dx=[

1

2

（1-k）x²-

1

3

x3]|

1-k 0

=

1

6

（1-k）³．
因此可得

1

6

（1-k）³=

4

81

，
解得k=

1

3

．
故选：A

点评：本题给出几何概型的概率，求直线的斜率k的值．着重考查了定积分计算公式、定积分的几何意义和几何概型公式等知识，属于中档题．