题目内容
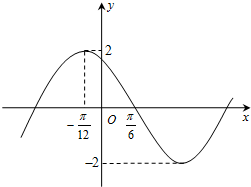 已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )
已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(6x-
| ||
D、f(x)=2sin(6x+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:计算题,三角函数的图像与性质
分析:由题设可得T=4(
+
)=π由公式可求得ω,再由图象经过点(-
,2),可求得φ,从而可求得函数f(x)的解析式.
| π |
| 6 |
| π |
| 12 |
| π |
| 12 |
解答:
解:由图象知T=4(
+
)=π.
∵T=
=π,∴ω=2.
又∵图象经过点(-
,2),
∴2sin(-
+φ)=2.
∵-π<φ<π,∴φ=
,
∴f(x)=2sin(2x+
).
故选:B.
| π |
| 6 |
| π |
| 12 |
∵T=
| 2π |
| ω |
又∵图象经过点(-
| π |
| 12 |
∴2sin(-
| π |
| 6 |
∵-π<φ<π,∴φ=
| 2π |
| 3 |
∴f(x)=2sin(2x+
| 2π |
| 3 |
故选:B.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得ω,φ是关键,也是难点,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(理)不等式4x2-7x-2<0成立的一个必要不充分条件是( )
A、(-
| ||
B、(-∞,-
| ||
C、(-
| ||
| D、(-1,2) |
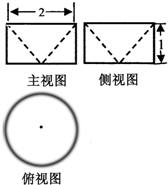 已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )
已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )| A、1:4 | B、1:2 |
| C、1:1 | D、2:1 |
执行如图所示的程序框图,输出的S值为( )


| A、2 | B、-2 | C、4 | D、-4 |
在△ABC中,已知
•
=4,|
|=3,M、N分别是BC边上的三等分点,则
•
的值是( )
| AB |
| AC |
| BC |
| AM |
| AN |
| A、5 | ||
B、
| ||
| C、6 | ||
| D、8 |
若Z=
(i为虚数单位),则Z的共轭复数为( )
| 2-i |
| 1+i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|