题目内容
2．已知函数f（x）=ax-2-2的图象恒过点P，且对数函数y=g（x）的图象过点P，则g（x）=log${\;}_{\frac{1}{2}}$x．分析 令x-2=0求出P点坐标，使用待定系数法求出g（x）．
解答 解：令x-2=0得x=2，∴f（x）恒过点（2，-1）．设g（x）=logax，则loga2=-1．解得a=$\frac{1}{2}$．
∴g（x）=log${\;}_{\frac{1}{2}}$x．
故答案为：${log_{\frac{1}{2}}}x$．
点评 本题考查了指数函数的性质及待定系数法求函数的解析式．是基础题．
练习册系列答案
相关题目
13．设等比数列{an}的前n项和为Sn，已知a1=1，q=2，则S10=（ ）
| A． | 1023 | B． | 2047 | C． | 511 | D． | 255 |
10．若函数$f（x）=2sin（ωx+\frac{π}{3}），x∈R$，又f（m）=-2，f（n）=0，且|m-n|的最小值为$\frac{3π}{4}$，则正数ω的值是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{3}{2}$ |
17．三个数a=0.36，b=60.7，c=log0.5$\frac{3}{2}$的大小关系为（ ）
| A． | a＞b＞c | B． | a＞c＞b | C． | b＞a＞c | D． | c＞a＞b |
7．与函数y=x是同一个函数的是（ ）
| A． | y=$\sqrt{x^2}$ | B． | y=$\frac{x^2}{x}$ | C． | $y={a^{{{log}_a}x}}$ | D． | y=logaax |
11．若用“五点法”画函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜π）的图象，其五点如下表：
（1）求函数f（x）的解析式；
（2）设g（x）=Acos（ωx+φ），若关于x的方程g（x）+λ=0在[π，7π]内恰有两个不同的解α，β，求实数λ的取值范围，并求α+β的值．
| x | $\frac{π}{2}$ | 2π | $\frac{7π}{2}$ | 5π | $\frac{13π}{2}$ |
| y | 0 | 2 | 0 | -2 | 0 |
（2）设g（x）=Acos（ωx+φ），若关于x的方程g（x）+λ=0在[π，7π]内恰有两个不同的解α，β，求实数λ的取值范围，并求α+β的值．
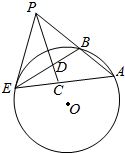如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE，BE，∠APE的平分线与AE，BE分别交于点C，D．