题目内容
14.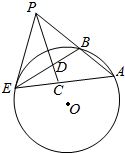 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.(1)求证:$\frac{DB}{DE}$=$\frac{PD}{PC}$;
(2)若∠PCE=2∠AEB,求∠PDB的大小.
分析 (1)由题意可知,∠EPC=∠APC,∠PEB=∠PAC,从而△PED∽△PAC,结合PD平分∠BPE,切割线定理,由此能证明$\frac{DB}{DE}$=$\frac{PD}{PC}$;
(2)由∠PCE=∠A+∠APC=∠PED+∠EPC=∠EDC=∠PDB,能求出∠PDB的大小.
解答 (1)证明:由题意可知,∠EPC=∠APC,∠PEB=∠PAC,
则△PED∽△PAC,则$\frac{PE}{PA}$=$\frac{PD}{PC}$①,
又PD平分∠BPE,∴$\frac{PE}{PB}$=$\frac{DE}{DB}$②,
∵PE2=PA•PB,
∴①×②可得:$\frac{DB}{DE}$=$\frac{PD}{PC}$(5分)
(2)解:∠PCE=∠A+∠APC=∠PED+∠EPC=∠EDC=∠PDB,
∴∠PCE+∠AEB+∠EDC=180°,
∴∠AEB=36°,
∴∠PDB=72°.(10分)
点评 本小题主要考查平面几何的证明,具体涉及到弦切角定理以及三角形相似等内容.本小题重点考查考生对平面几何推理能力.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
3.已知:在平面Rt△ABC,∠C=90°,动点P满足|PC|+|CB|=|PA|+|AB|,则点P的轨迹是( )
| A. | 椭圆 | B. | 双曲线 | C. | 双曲线的一支 | D. | 抛物线 |
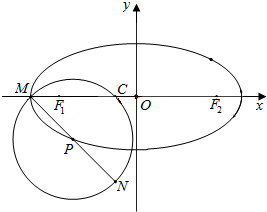 已知椭圆E的方程:$\frac{x^2}{100}+\frac{y^2}{25}=1$,P为椭圆上的一点(点P在第三象限上),圆P 以点P为圆心,且过椭圆的左顶点M与点C(-2,0),直线MP交圆P与另一点N.
已知椭圆E的方程:$\frac{x^2}{100}+\frac{y^2}{25}=1$,P为椭圆上的一点(点P在第三象限上),圆P 以点P为圆心,且过椭圆的左顶点M与点C(-2,0),直线MP交圆P与另一点N.