题目内容
国庆期间襄阳某体育用品专卖店抓住商机大量购进某特许商品进行销售,该特许产品的成本为20元/个,每日的销售量y(单位:个)与单价x(单位:元)之间满足关系式y=
+4(x-50)2,(其中20<x<50,a为常数).当销售价格为40元/个时,每日可售出该商品401个.
(1)求a的值及每日销售该特许产品所获取的总利润L(x);
(2)试确定单价x的值,使所获得的总利润L(x)最大.
| a |
| x-20 |
(1)求a的值及每日销售该特许产品所获取的总利润L(x);
(2)试确定单价x的值,使所获得的总利润L(x)最大.
考点:利用导数求闭区间上函数的最值
专题:计算题,应用题,导数的综合应用
分析:(1)由题意401=
+4•(40-50)2,从而求出参数值,再写出总利润L(x)即可;
(2)化简L(x)=4x3-480x2+18000x-199980,求导L′(x)=12(x-30)(x-50),讨论其正负从而确定单调性,从而求最值.
| a |
| 40-20 |
(2)化简L(x)=4x3-480x2+18000x-199980,求导L′(x)=12(x-30)(x-50),讨论其正负从而确定单调性,从而求最值.
解答:
解:(1)∵y=
+4(x-50)2,
∴401=
+4•(40-50)2,
解得,a=20;
∴y=
+4(x-50)2,
则每日销售该特许产品所获取的总利润
L(x)=y(x-20)=(
+4(x-50)2)(x-20)=20+4(x-20)•(x-50)2,(20<x<50)
(2)由L(x)=20+4(x-20)•(x-50)2=4x3-480x2+18000x-199980,
L′(x)=12x2-960x+18000=12(x-30)(x-50),
则当x∈(20,30)时,L′(x)>0,L(x)为增函数;
当x∈(30,50)时,L′(x)<0,L(x)为减函数;
则当x=30时,Lmax(x)=16020.
即当销售单价为30元/个时,
所获得的总利润最大,为16020元.
| a |
| x-20 |
∴401=
| a |
| 40-20 |
解得,a=20;
∴y=
| 20 |
| x-20 |
则每日销售该特许产品所获取的总利润
L(x)=y(x-20)=(
| 20 |
| x-20 |
(2)由L(x)=20+4(x-20)•(x-50)2=4x3-480x2+18000x-199980,
L′(x)=12x2-960x+18000=12(x-30)(x-50),
则当x∈(20,30)时,L′(x)>0,L(x)为增函数;
当x∈(30,50)时,L′(x)<0,L(x)为减函数;
则当x=30时,Lmax(x)=16020.
即当销售单价为30元/个时,
所获得的总利润最大,为16020元.
点评:本题考查了将实际问题转化为数学问题的能力及导数的综合应用,属于中档题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤| π |
| 2 |
A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(x+
|
设圆柱的表面积为S,当圆柱体积最大时,圆柱的高为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、3π
|
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式与S=f(0)+f(1)+f(2)+…+f(2010)的值分别为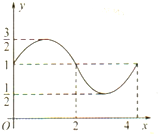 ( )
( )
 ( )
( )A、f(x)=
| ||||||
B、f(x)=sin
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
 如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.
如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.