Question

函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式与S=f（0）+f（1）+f（2）+…+f（2010）的值分别为（　　）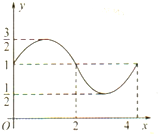

• A、f（x）=

  1

  2

  sin2πx+1，S=2010
• B、f（x）=sin

  π

  2

  x+1，S=2011

  1

  2

• C、f（x）=

  1

  2

  sin

  π

  2

  x+1，S=2010

  1

  2

• D、f（x）=

  1

  2

  sin

  π

  2

  x+1，S=2011

Answer 1

考点：正弦函数的图象

专题：三角函数的图像与性质

分析：由图象可求得f（x）=

1

2

sin

π

2

x+1，再利用其周期性计算f（0）+f（1）+f（2）+f（3）的值，从而可得答案．

解答： 解：观察图象知b=1，T=4=

2π

ω

，
∴ω=

π

2

，又A=

1

2

，
∴f（x）=

1

2

sin

π

2

x+1，
∴f（0）=1，f（1）=

3

2

，f（2）=1，f（3）=

1

2

，f（4）=1，且以4为周期，
f（0）+f（1）+f（2）+f（3）=4，
∴S=f（0）+f（1）+f（2）+…+f（2010）=4×503-f（3）=2012-

1

2

=2011

1

2

故选：B．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查三角函数的恒等变换及化简求值，考查函数的周期性，属于中档题．