题目内容
在△ABC中，内角A，B，C对边的边长分别是a，b，c，2
sin
cos
+2cos2
=3．
（1）求角A；
（2）若a=
，sin（B+C）+sin（B-C）=2sin2C，cosC≠0，求△ABC的面积．
| 3 |
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
（1）求角A；
（2）若a=
| 3 |
考点：两角和与差的正弦函数,余弦定理
专题：解三角形
分析：（1）先利用倍角公式降幂，再利用两角和的正弦化简，然后结合A的范围求解A的值；
（2）利用两角和与差的正弦展开等式左边，右边展开二倍角正弦，化简后由角的关系得到边的关系，再结合余弦定理求得b，c的值，然后代入面积公式求面积．
（2）利用两角和与差的正弦展开等式左边，右边展开二倍角正弦，化简后由角的关系得到边的关系，再结合余弦定理求得b，c的值，然后代入面积公式求面积．
解答：
解：（1）由2
sin
cos
+2cos2
=3．
得
sinA+cosA+1=3，即
sinA+cosA=2．
∴2(sinAcos
+cosAsin
)=1，
sin(A+
)=1．
∵A∈（0，π），
∴A+
=
，得A=
；
（2）由sin（B+C）+sin（B-C）=2sin2C，
得：sinBcosC+cosBsinC+sinBcosC-cosBsinC=2sin2C．
2sinBcosC=4sinCcosC．
∴sinB=2sinC．
则b=2c ①．
又a=
，
由a2=b2+c2-2bccosA，
得：(
)2=b2+c2-2bccos
，
即b2+c2-bc=3 ②．
联立①②解得：b=2，c=1．
∴S△ABC=
bcsinA=
×2×1×
=
．
| 3 |
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
得
| 3 |
| 3 |
∴2(sinAcos
| π |
| 6 |
| π |
| 6 |
sin(A+
| π |
| 6 |
∵A∈（0，π），
∴A+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
（2）由sin（B+C）+sin（B-C）=2sin2C，
得：sinBcosC+cosBsinC+sinBcosC-cosBsinC=2sin2C．
2sinBcosC=4sinCcosC．
∴sinB=2sinC．
则b=2c ①．
又a=
| 3 |
由a2=b2+c2-2bccosA，
得：(
| 3 |
| π |
| 3 |
即b2+c2-bc=3 ②．
联立①②解得：b=2，c=1．
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评：本题考查两角和与差的正弦函数，考查了倍角公式，考查了余弦定理的应用，训练了三角形面积的求法，是中档题．
练习册系列答案
相关题目
已知双曲线
-
=1的离心率为e，焦点为F的抛物线y2=2px与直线y=k（x-
）交于A，B两点，且
=e，则k的值为（ ）
| x2 |
| 4 |
| y2 |
| 12 |
| p |
| 2 |
| 丨AF丨 |
| 丨BF丨 |
A、2
| ||
B、2
| ||
C、±2
| ||
D、±2
|
若复数
-1（a为实数，i为虚数单位）是纯虚数，则a=（ ）
| a+i |
| 3+4i |
| A、7 | ||
| B、-7 | ||
C、
| ||
D、-
|
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．
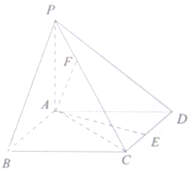如图，已知四棱锥，底面ABCD为菱形，PA⊥平面ABCD，PA=AB=2，∠ABC=60°，E是CD的中点，F为PC上一点，满足FC=2PF．
如图，在棱长为2的正方体ABCD-A1B1C1D1中，E，F，M，N分别是棱AB，AD，A1B1，A1D1的中点，点P，Q分别在棱DD1，BB1上移动，且DP=BQ=λ（0＜λ＜2）