题目内容
已知函数f(x)=x3+3x|x-a|.
(1)当a=
时,求函数f(x)的单调递增区间;
(2)若f(x)在区间[0,2]内有极小值,且极小值不小于2a2-
a,求实数a的取值范围.
(1)当a=
| 1 |
| 2 |
(2)若f(x)在区间[0,2]内有极小值,且极小值不小于2a2-
| 3 |
| 4 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)将函数转化为分段函数,再利用导数确定函数的单调递增区间;
(2)由x∈[0,2],比较a与0,2的大小将函数转化为分段函数;再逐段利用导数确定函数的单调性,从而确定函数的极小值.
(2)由x∈[0,2],比较a与0,2的大小将函数转化为分段函数;再逐段利用导数确定函数的单调性,从而确定函数的极小值.
解答:
解:(1)当a=
时,f(x)=
,f′(x)=
,
解不等式组
得x>
; 解不等式组
得x<
.
∴f(x)的递增区间为(-∞,
)和(
,+∞).
(2)①当a≥2时,由0≤x≤2得f(x)=x3-3x2+3ax,f′(x)=3x2-6x+3a=3(x-1)2+3(a-1)>0,
∴f(x)在区间[0,2]上递增,∴f(x)没有极值.
②当a≤0时,由0≤x≤2得f(x)=x3+3x2-3ax,f′(x)=3x2+6x-3a>0,
∴f(x)在区间[0,2]上递增,∴f(x)没有极值.
③当1≤a<2时,f(x)=
,f′(x)=
,
∴f′(x)=
,
∴f(x)在区间[0,2]上递增,∴f(x)没有极值.
④当0<a<1时,f(x)=
,f′(x)=
,
若x≥a,则 f′(x)=3x2+3x+3(x-a)>0;
若x<a,由f′(x)=3x2-6x+3a>0解得x>1+
或 x<1-
,∴x<1-
,
由f′(x)=3x2-6x+3a<0解得1-
<x<1+
,∴1-
<x<a,
∴f(x)在区间(0,1-
)上递增,在区间(1-
,a)上递减,在区间(a,2)上递增.
∴当x=a时,f(x)取得极小值f(a)=a3,∴a3≥2a2-
a,解得0<a≤
.
综上所述,实数a的取值范围为(0,
].
| 1 |
| 2 |
|
|
解不等式组
|
| 1 |
| 2 |
|
2-
| ||
| 2 |
∴f(x)的递增区间为(-∞,
2-
| ||
| 2 |
| 1 |
| 2 |
(2)①当a≥2时,由0≤x≤2得f(x)=x3-3x2+3ax,f′(x)=3x2-6x+3a=3(x-1)2+3(a-1)>0,
∴f(x)在区间[0,2]上递增,∴f(x)没有极值.
②当a≤0时,由0≤x≤2得f(x)=x3+3x2-3ax,f′(x)=3x2+6x-3a>0,
∴f(x)在区间[0,2]上递增,∴f(x)没有极值.
③当1≤a<2时,f(x)=
|
|
∴f′(x)=
|
∴f(x)在区间[0,2]上递增,∴f(x)没有极值.
④当0<a<1时,f(x)=
|
|
若x≥a,则 f′(x)=3x2+3x+3(x-a)>0;
若x<a,由f′(x)=3x2-6x+3a>0解得x>1+
| 1-a |
| 1-a |
| 1-a |
由f′(x)=3x2-6x+3a<0解得1-
| 1-a |
| 1-a |
| 1-a |
∴f(x)在区间(0,1-
| 1-a |
| 1-a |
∴当x=a时,f(x)取得极小值f(a)=a3,∴a3≥2a2-
| 3 |
| 4 |
| 1 |
| 2 |
综上所述,实数a的取值范围为(0,
| 1 |
| 2 |
点评:本题考查了利用导数确定函数单调性与极值的方法.根据a是否在区间[0,2]内以及导数为0的点是否在区间[0,2]内是分类求解的基本依据,也是解决本题的关键所在.

练习册系列答案
相关题目
若复数
+
(i为虚数单位)的实部与虚部互为相反数,则实数a的值为( )
| a |
| 1-i |
| 1-i |
| 2 |
| A、2 | B、1 | C、-1 | D、0 |
已知sinα=
,则cos2α-cos2α的值为( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.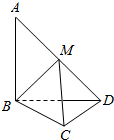 在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.