题目内容
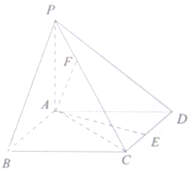 如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.
如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.(1)证明:AE⊥PB;
(2)求直线AF与平面PCD所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)通过已知条件证明AE⊥平面PAB,进而可得直线与直线的垂直;
(2)过A作AM⊥PE,垂足为M,可证∠AFM即为直线线AF与平面PCD所成角,分别在RT△PAE和RT△PAC中,求解AM和AF,由正弦函数的定义可得.
(2)过A作AM⊥PE,垂足为M,可证∠AFM即为直线线AF与平面PCD所成角,分别在RT△PAE和RT△PAC中,求解AM和AF,由正弦函数的定义可得.
解答:
解:(1)∵四边形ABCD为菱形,∠ABC=60°,
∴△ACD为正三角形,
∵E是CD的中点,∴AE⊥CD,
又∵AB∥CD,∴AE⊥AB,
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE,
又AB?平面PAB,PA?平面PAB且PA∩AB=A,
∴AE⊥平面PAB,又PB?平面PAB,
∴AE⊥PB
(2)∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD,
∵AE⊥CD,PA?平面PAE,AE?平面PAE,且AE∩PA=A,
∴CD⊥平面PAE,又CD?平面PCD,∴平面PCD⊥平面PAE,
过A作AM⊥PE,垂足为M,又平面PCD∩平面PAE=PE,AM?平面PAE,
∴AM⊥平面PCD,∠AFM即为直线线AF与平面PCD所成角,
在RT△PAE中,AE=
AB=
,PA=2,∴AM=
,
在RT△PAC中,AC=AB=2,PA=2,∴AF=
,
在RT△AMF中,sin∠AFM=
=
,
∴直线AF与平面PCD所成角的正弦值为:
∴△ACD为正三角形,
∵E是CD的中点,∴AE⊥CD,
又∵AB∥CD,∴AE⊥AB,
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE,
又AB?平面PAB,PA?平面PAB且PA∩AB=A,
∴AE⊥平面PAB,又PB?平面PAB,
∴AE⊥PB
(2)∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD,
∵AE⊥CD,PA?平面PAE,AE?平面PAE,且AE∩PA=A,
∴CD⊥平面PAE,又CD?平面PCD,∴平面PCD⊥平面PAE,
过A作AM⊥PE,垂足为M,又平面PCD∩平面PAE=PE,AM?平面PAE,
∴AM⊥平面PCD,∠AFM即为直线线AF与平面PCD所成角,
在RT△PAE中,AE=
| ||
| 2 |
| 3 |
2
| ||
| 7 |
在RT△PAC中,AC=AB=2,PA=2,∴AF=
2
| ||
| 3 |
在RT△AMF中,sin∠AFM=
| AM |
| AF |
3
| ||
| 35 |
∴直线AF与平面PCD所成角的正弦值为:
3
| ||
| 35 |
点评:本题考查直线与平面的位置关系,涉及线面角和垂直的判定和性质,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)=sin(2x+φ)(0<φ<π),f(x)图象的一条对称轴是x=
,则φ的值为( )
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4 |
| 2015 |
| 2014 |
| 2015 |
| A、1007 | B、2014 |
| C、2015 | D、4028 |
已知sinα=
,则cos2α-cos2α的值为( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
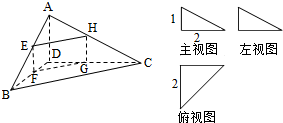 四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H.
四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H. 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.