题目内容
已知函数f(x)=
x3+x2+ax+1(a∈R).
(1)求函数f(x)的单调区间;
(2)当a<0时,试讨论是否存在x0∈(0,
)∪(
,1),使得f(x0)=f(
).
| 1 |
| 3 |
(1)求函数f(x)的单调区间;
(2)当a<0时,试讨论是否存在x0∈(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:函数的性质及应用,导数的综合应用
分析:对第(1)问,先求导,再通过一元二次方程的实根讨论单调性;
对第(2)问,可将f(x0)=f(
)转化为f(x0)-f(
)=0,即将“函数问题”化为“方程是否有实根问题”处理.
对第(2)问,可将f(x0)=f(
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)由f(x)得f′(x)=x2+2x+a,
令f′(x)=0,即x2+2x+a=0,判别式△=4-4a,
①当△≤0即a≥1时,f′(x)≥0,则f(x)在(-∞,+∞)上为增函数.
②当△>0即a<1时,方程f′(x)=0的两根为
,即-1±
,
当x∈(-∞,-1-
)时,f′(x)>0,则f(x)为增函数;
当x∈(-1-
,-1+
)时,f′(x)<0,则f(x)为减函数;
当x∈(-1+
,+∞)时,f′(x)>0,则f(x)为增函数.
综合①、②知,a≥1时,f(x)的单调递增区间为(-∞,+∞),
a<1时,f(x)的单调递增区间为(-∞,-1-
)和(-1+
,+∞),
f(x)的单调递减区间为(-1-
,-1+
).
(2)∵f(x)-f(
)=
x3+x2+ax+1-[
×(
)3+(
)2+a×
+1]
=
[x3-(
)3]+[x2-(
)2]+a(x-
)
=
[(x-
)(x2+
+
)]+(x+
)(x-
)+a(x-
)
=(x-
)(
+
+
+a)
=
(x-
)(4x2+14x+7+12a).
∴若存在x0∈(0,
)∪(
,1),使得f(x0)=f(
),即f(x0)-f(
)=0,
则关于x的方程4x2+14x+7+12a=0在(0,
)∪(
,1)内必有实数解.
∵a<0,∴△=142-16(7+12a)=4(21-48a)>0,
方程4x2+14x+7+12a=0的两根为
,即
,
∵x0>0,∴x0=
,
依题意有0<
<1,且
≠
,
即7<
<11,且
≠9,∴49<21-48a<121,且21-48a≠81,
得-
<a<-
,且a≠-
.
∴当a∈(-
,-
)∪(-
,-
)时,存在唯一的x0∈(0,
)∪(
,1),使得f(x0)=f(
)成立;
当a∈(-∞,-
]∪[-
,0)∪{-
}时,不存在x0∈(0,
)∪(
,1),使得f(x0)=f(
)成立.
令f′(x)=0,即x2+2x+a=0,判别式△=4-4a,
①当△≤0即a≥1时,f′(x)≥0,则f(x)在(-∞,+∞)上为增函数.
②当△>0即a<1时,方程f′(x)=0的两根为
-2±
| ||
| 2 |
| 1-a |
当x∈(-∞,-1-
| 1-a |
当x∈(-1-
| 1-a |
| 1-a |
当x∈(-1+
| 1-a |
综合①、②知,a≥1时,f(x)的单调递增区间为(-∞,+∞),
a<1时,f(x)的单调递增区间为(-∞,-1-
| 1-a |
| 1-a |
f(x)的单调递减区间为(-1-
| 1-a |
| 1-a |
(2)∵f(x)-f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=(x-
| 1 |
| 2 |
| x2 |
| 3 |
| 7x |
| 6 |
| 7 |
| 12 |
=
| 1 |
| 12 |
| 1 |
| 2 |
∴若存在x0∈(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则关于x的方程4x2+14x+7+12a=0在(0,
| 1 |
| 2 |
| 1 |
| 2 |
∵a<0,∴△=142-16(7+12a)=4(21-48a)>0,
方程4x2+14x+7+12a=0的两根为
-14±2
| ||
| 8 |
-7±
| ||
| 4 |
∵x0>0,∴x0=
-7+
| ||
| 4 |
依题意有0<
-7+
| ||
| 4 |
-7+
| ||
| 4 |
| 1 |
| 2 |
即7<
| 21-48a |
| 21-48 a |
得-
| 25 |
| 12 |
| 7 |
| 12 |
| 5 |
| 4 |
∴当a∈(-
| 25 |
| 12 |
| 5 |
| 4 |
| 5 |
| 4 |
| 7 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当a∈(-∞,-
| 25 |
| 12 |
| 7 |
| 12 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:1.求含参数的函数的单调区间时,导函数的符号往往难以确定,如果受到参数的影响,应对参数进行讨论,讨论的标准要根据导函数解析式的特征而定.如本题中导函数为一元二次函数,就有必要考虑对应方程中的判别式△.
2.对于存在性问题,一般先假设所判断的问题成立,再由假设去推导,若求得符合题意的结果,则存在;若得出矛盾,则不存在.
2.对于存在性问题,一般先假设所判断的问题成立,再由假设去推导,若求得符合题意的结果,则存在;若得出矛盾,则不存在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若不等式lg
≥(x-1)lg3对任意x∈(-∞,1)恒成立,则a的取值范围是( )
| 1+2x+(1-a)3x |
| 3 |
| A、(-∞,0] |
| B、[1,+∞) |
| C、[0,+∞) |
| D、(-∞,1] |
设b、c分别是先后抛掷一枚骰子得到的点数,则函数f(x)=x2+bx+c有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.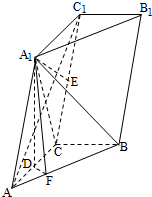 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.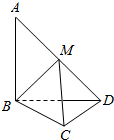 在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.