Question

如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E，F，M，N分别是棱AB，AD，A₁B₁，A₁D₁的中点，点P，Q分别在棱DD₁，BB₁上移动，且DP=BQ=λ（0＜λ＜2）
（Ⅰ）当λ=1时，证明：直线BC₁∥平面EFPQ；
（Ⅱ）是否存在λ，使面EFPQ与面PQMN所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面平行的判定

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）建立坐标系，求出

BC1

=2

FP

，可得BC₁∥FP，利用线面平行的判定定理，可以证明直线BC₁∥平面EFPQ；
（Ⅱ）求出平面EFPQ的一个法向量、平面MNPQ的一个法向量，利用面EFPQ与面PQMN所成的二面角为直二面角，建立方程，即可得出结论．

解答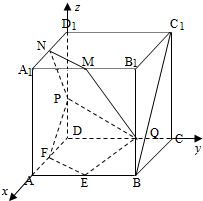： （Ⅰ）证明：以D为原点，射线DA，DC，DD₁分别为x，y，z轴的正半轴，建立坐标系，则B（2，2，0），C₁（0，2，2），E（2，1，0），F（1，0，0），P（0，0，λ），
∴

BC1

=（-2，0，2），

FP

=（-1，0，λ），

FE

=（1，1，0）
λ=1时，

BC1

=（-2，0，2），

FP

=（-1，0，1），
∴

BC1

=2

FP

，
∴BC₁∥FP，
∵FP?平面EFPQ，BC₁?平面EFPQ，
∴直线BC₁∥平面EFPQ；
（Ⅱ）设平面EFPQ的一个法向量为

m

=（x，y，z），则

x+y=0 -x+λz=0

，
∴取

m

=（λ，-λ，1）．
同理可得平面MNPQ的一个法向量为

n

=（λ-2，2-λ，1），
若存在λ，使面EFPQ与面PQMN所成的二面角为直二面角，则

m

•

n

=λ（λ-2）-λ（2-λ）+1=0，∴λ=1±

2

2

．
∴存在λ=1±

2

2

，使面EFPQ与面PQMN所成的二面角为直二面角．

点评：本题考查直线与平面平行的证明，考查存在性问题，解题时要合理地化空间问题为平面问题，注意向量法的合理运用．