题目内容
设f(x)=x|x-1|-blnx+m,(b,m∈R)
(Ⅰ)当b=3时,判断函数f(x)在[l,+∞)上的单调性;
(Ⅱ)记h(x)=f(x)+blnx,当m>1时,求函数y=h(x)在[0,m]上的最大值;
(Ⅲ)当b=1时,若函数f(x)有零点,求实数m的取值范围.
(Ⅰ)当b=3时,判断函数f(x)在[l,+∞)上的单调性;
(Ⅱ)记h(x)=f(x)+blnx,当m>1时,求函数y=h(x)在[0,m]上的最大值;
(Ⅲ)当b=1时,若函数f(x)有零点,求实数m的取值范围.
考点:函数零点的判定定理,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)求出f′(x)=
=
,解不等式即可.
(2)分类讨论当x∈[0,1]时,h(x)=-(x-
)2+m+
,当x∈(1,m]时,h(x)=(x-
)2+m-
,再利用单调性求解最值.
(3)转化为m=lnx-x|x-1|有解,构造函数g(x)=lnx-x|x-1|,利用导数判断单调性,借助最值研究.
| 2x2-x-3 |
| x |
| (2x-3)(x+1) |
| x |
(2)分类讨论当x∈[0,1]时,h(x)=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
(3)转化为m=lnx-x|x-1|有解,构造函数g(x)=lnx-x|x-1|,利用导数判断单调性,借助最值研究.
解答:
解:(1)当b=3时,因为x>1,则f(x)=x2-x-3lnx+m,
f′(x)=
=
,
当x≥
时,f′(x)>0,所以f(x)在[
,+∞)单调递增
当x∈[1,
]时,f′(x)<0,所以f(x)在[1,
)单调递减
(2)h(x)=f(x)+m,
∴当x∈[0,1]时,h(x)=-(x-
)2+m+
,
∴当x=
时,h(x)min=m+
∵h(x)∈在(1,m]单调递增,
∴h(x)max=m2
由2≥m+
,
又m>1,
∴可得m≥
,
∴当m≥
时,h(x)max=m2,
当1<m<
时,h(x)max=m+
(3)b=1时,函数f(x)有零点,即x|x-1|-lnx+m=0有解,
即当x∈(0,1]时,g(x)=x2-x+lnx,
∵g′(x)=2x-1+
≥2
-1>0,
∴g(x)=lnx-x|x-1|,在(0,1]单调递增,
∴g(x)≤g(1)=0
=-
<0,
当x∈(1,+∞)时,g(x)=-x2+x+lnx,
g′(x)=-
<0,
∴g(x)=lnx-x|x-1|,在(1,+∞)单调递减,
∴g(x)<g(1)=0
∴m=lnx-x|x-1|有解时,实数的取值范围为:m≤0
f′(x)=
| 2x2-x-3 |
| x |
| (2x-3)(x+1) |
| x |
当x≥
| 3 |
| 2 |
| 3 |
| 2 |
当x∈[1,
| 3 |
| 2 |
| 3 |
| 2 |
(2)h(x)=f(x)+m,
∴当x∈[0,1]时,h(x)=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
∴当x=
| 1 |
| 2 |
| 1 |
| 4 |
∵h(x)∈在(1,m]单调递增,
∴h(x)max=m2
由2≥m+
| 1 |
| 4 |
又m>1,
∴可得m≥
1+
| ||
| 2 |
∴当m≥
1+
| ||
| 2 |
当1<m<
1+
| ||
| 2 |
| 1 |
| 4 |
(3)b=1时,函数f(x)有零点,即x|x-1|-lnx+m=0有解,
即当x∈(0,1]时,g(x)=x2-x+lnx,
∵g′(x)=2x-1+
| 1 |
| x |
| 2 |
∴g(x)=lnx-x|x-1|,在(0,1]单调递增,
∴g(x)≤g(1)=0
=-
| (x-1)(2x+1) |
| x |
当x∈(1,+∞)时,g(x)=-x2+x+lnx,
g′(x)=-
| (x-1)(2x+1) |
| x |
∴g(x)=lnx-x|x-1|,在(1,+∞)单调递减,
∴g(x)<g(1)=0
∴m=lnx-x|x-1|有解时,实数的取值范围为:m≤0
点评:本题综合考察了函数的单调性,零点,不等式等知识,属于难题.

练习册系列答案
相关题目
已知集合A={x|-1≤x<3},B={x|2<x≤5},则A∩B=( )
| A、(2,3) |
| B、[-1,5] |
| C、(-1,5) |
| D、(-1,5] |
已知双曲线的中心在原点,焦点在x轴上,一条渐进线方程是y=
x,那么它的离心率是( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
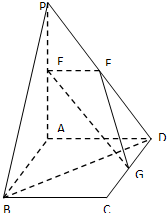 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.