题目内容
已知A(1,1),B(1,0),P为椭圆
+
=1上任意一点,则|PA|+2|PB|的最小值为 .
| x2 |
| 4 |
| y2 |
| 3 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用椭圆的定义,|PA|+2|PB|=PA+d,利用三点共线,即可得出结论.
解答:
解:椭圆
+
=1中,a2=4,a=2,b2=3,c2=a2-b2=1,c=1,
∴点B为椭圆的右焦点.
设P到右准线距离为d,那么
=e=
,∴d=2PB,
∴PA+2PB=PA+d,
点A在椭圆内,过点A与x轴平行的直线y=1交右准线于C,
∵右准线x=4,
∴PA+2PB=PA+PC=4-1=3即为所求.
故答案为:3
| x2 |
| 4 |
| y2 |
| 3 |
∴点B为椭圆的右焦点.
设P到右准线距离为d,那么
| PB |
| d |
| 1 |
| 2 |
∴PA+2PB=PA+d,
点A在椭圆内,过点A与x轴平行的直线y=1交右准线于C,
∵右准线x=4,
∴PA+2PB=PA+PC=4-1=3即为所求.
故答案为:3
点评:本题考查椭圆的性质,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数为幂函数的是( )
①y=x2+1; ②y=2x; ③y=
; ④y=(x-1)2; ⑤y=x5; ⑥y=xx+1.
①y=x2+1; ②y=2x; ③y=
| 1 |
| x2 |
| A、①③⑤ | B、①②⑤ |
| C、③⑤ | D、④⑤⑥ |
如图所示是四棱锥的三视图,则该几何的体积等于( )

| A、16 | ||
B、34+6
| ||
| C、6 | ||
D、17+6
|
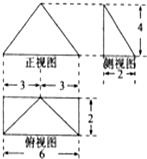
一个几何体的三视图如图所示,则这个几何体的体积为( )


| A、6.5 | B、7 | C、7.5 | D、8 |
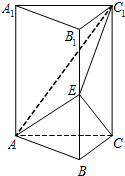 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=