题目内容
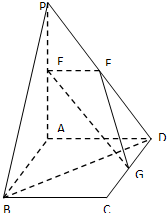 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.(1)求证:PB∥平面EFG
(2)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离为0.8,若存在,求出CQ的长,若不存在,请说明理由.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:空间位置关系与距离
分析:对第(1)问,设AC∩BD=0,连结OF,只需证平面EFG外的一条线PB平行于平面内的直线OF即可.
对第(2)问,由PA,AB,AD两两垂直,以AB,AD,AP分别为x轴,y轴,z轴的正方向建立空间直角坐标系,先假设存在满足题意的点Q(x0,2,0),根据点A到平面EFQ的距离为0.8,再将此距离转化为向量
在平面EFQ的法向量方向上的射影长,从而得到关于x0的方程,通过解方程即可探求点Q的存在性.
对第(2)问,由PA,AB,AD两两垂直,以AB,AD,AP分别为x轴,y轴,z轴的正方向建立空间直角坐标系,先假设存在满足题意的点Q(x0,2,0),根据点A到平面EFQ的距离为0.8,再将此距离转化为向量
| AE |
解答:
解:(1)证:连结AC,设AC∩BD=0,连结OF,0G,则OG∥BC∥AD∥EF,∴E,F,G,O四点共面,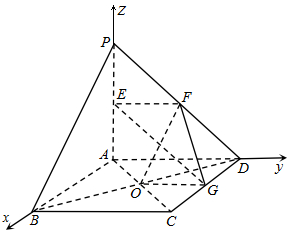
∵OF∥PB,PB?平面EFG,OF?平面EFG,
∴PB∥平面EFG.
(2)由题意易得PA,AB,AD两两垂直,以AB,AD,AP分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如右图所示,则点E(0,0,1),F(0,1,1).
假设在线段CD上,存在一点Q(x0,2,0)满足题意,则
=(0,1,0),
=(x0,2,-1),
=(0,0,-1).又设平面EFQ的法向量为
=(x,y,z),则有
,即
,
∴y=0,z=x0x.取x=1,得
=(1,0,x0),则
在平面EFQ的法向量方向上的射影长
=0.8,
得x02=(
)2+(
)2x02,
又∵x0>0,得x0=
,∴Q(
,2,0),从而
=(-
,0,0),
∴|CQ|=
,即在线段CD上存在一点Q满足题意,且CQ的长为
.

∵OF∥PB,PB?平面EFG,OF?平面EFG,
∴PB∥平面EFG.
(2)由题意易得PA,AB,AD两两垂直,以AB,AD,AP分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如右图所示,则点E(0,0,1),F(0,1,1).
假设在线段CD上,存在一点Q(x0,2,0)满足题意,则
| EF |
| EQ |
| EA |
| u |
|
|
∴y=0,z=x0x.取x=1,得
| u |
| EA |
|
| ||||
|
|
得x02=(
| 4 |
| 5 |
| 4 |
| 5 |
又∵x0>0,得x0=
| 4 |
| 3 |
| 4 |
| 3 |
| CQ |
| 2 |
| 3 |
∴|CQ|=
| 2 |
| 3 |
| 2 |
| 3 |
点评:1.本题考查了线面平行的判定定理,证线面平行的关键是:在已知平面内找一条线与已知直线平行,即将线面平行问题转化为线线平行问题,而线线平行常根据三角形中位线的性质或平行四边形的性质得证.
2.若涉及到三条两两垂直的直线,可以考虑建立空间直角坐标系.利用向量法求解点到平面距离问题时,一般将此距离转化为该点到平面内任意一点连线的向量在该平面法向量方向上的射影长处理.
2.若涉及到三条两两垂直的直线,可以考虑建立空间直角坐标系.利用向量法求解点到平面距离问题时,一般将此距离转化为该点到平面内任意一点连线的向量在该平面法向量方向上的射影长处理.

练习册系列答案
相关题目
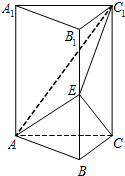 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=