题目内容
若n∈N*,求证
+
+…+
<
(n+2)2.
| 1×4 |
| 2×5 |
| n(n+3) |
| 1 |
| 2 |
考点:不等式的证明
专题:推理和证明
分析:通过不等式的左侧的最后一项,利用基本不等式放大,然后求和即可.
解答:
证明:由题意可知
<
=n+
,
∴
+
+…+
<(1+
)+(2+
)+(3+
)+…+(n+
)
=
n+(1+2+3+…+n)
=
n+
=
n2+2n<
n2+2n+2
=
(n+2)2.
∴n∈N*,
+
+…+
<
(n+2)2.恒成立.
| n(n+3) |
| n+n+3 |
| 2 |
| 3 |
| 2 |
∴
| 1×4 |
| 2×5 |
| n(n+3) |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
=
| 3 |
| 2 |
=
| 3 |
| 2 |
| n(n+1) |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
∴n∈N*,
| 1×4 |
| 2×5 |
| n(n+3) |
| 1 |
| 2 |
点评:本题考查不等式的证明,放缩法的应用,与自然数有关的命题也可以利用数学归纳法证明.考查逻辑推理能力以及计算能力.

练习册系列答案
相关题目
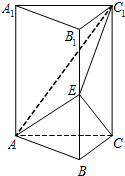 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=