题目内容
19.直线l:y=k(x+2)被圆O:x2+y2=4截得弦长为2,则k值是±$\sqrt{3}$.分析 圆x2+y2=4的圆心为(0,0),半径为2,直线x-y=0过圆心,即可求出结果.
解答 解:圆x2+y2=4的圆心为(0,0),半径为2,
∵直线l:y=k(x+2)被圆O:x2+y2=4截得弦长为2,
∴圆心到直线的距离d=$\sqrt{4-1}$=$\sqrt{3}$,
∴圆心到直线的距离$\frac{|2k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{3}$,
∴k=±$\sqrt{3}$.
故答案为:±$\sqrt{3}$.
点评 本题是基础题,考查直线与圆的位置关系,弦长的求法,考查计算能力.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
9.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≥2\\ 2x+y≤4\\ y≤2\end{array}\right.$则目标函数z=3x-y的最大值( )
| A. | 6 | B. | $\frac{3}{2}$ | C. | -1 | D. | $-\frac{3}{2}$ |
10.已知圆C:(x-1)2+(y-2)2=2与y轴在第二象限所围区域的面积为S,直线y=2x+b分圆C的内部为两部分,其中一部分的面积也为S,则b=( )
| A. | $-\sqrt{6}$ | B. | ±$\sqrt{6}$ | C. | $-\sqrt{5}$ | D. | ±$\sqrt{5}$ |
7.已知A(2,0),B(-2,0),P(x,y),下列命题正确的是( )
| A. | 若P到A,B距离之和为4,则点P的轨迹为椭圆 | |
| B. | 若P到A,B距离之差为3,则点P的轨迹为双曲线 | |
| C. | 椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上任意一点M(长轴端点除外)与A,B连线斜率之积是-$\frac{3}{4}$ | |
| D. | 双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1上任意一点M(实轴端点除外)与A,B连线斜率之积是-$\frac{3}{4}$ |
14.在△ABC中,角A,B,C所对边分别为a,b,c,且(2b-a)•cosC=ccosA,c=3,sinA+sinB=2$\sqrt{6}$sinAsinB,则△ABC的面积为( )
| A. | $\frac{3\sqrt{3}}{8}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{4}$ |
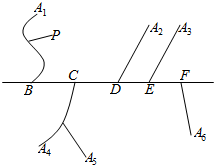 如图,一条公路的两侧有六个村庄,要建一个车站,要求到六个村庄的路程之和最小,应该选在哪里最合适?如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,那么这时车站设在什么地方好?
如图,一条公路的两侧有六个村庄,要建一个车站,要求到六个村庄的路程之和最小,应该选在哪里最合适?如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,那么这时车站设在什么地方好?