题目内容
4.M为何值时,直线2x-y+m=0与圆x2+y2=5(1)无公共点;
(2)截得弦长为2.
分析 (1)求出圆x2+y2=5圆心到直线2x-y+m=0的距离d,由直线与圆无公共点,得d>r,由此能求出m的取值范围.
(2)由平面几何垂径定理得到r2-d2=12,由此能求出直线被圆截得的弦长为2的m值.
解答 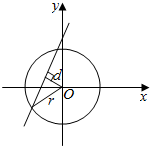 解:(1)∵圆x2+y2=5圆心为O(0,0),半径r=$\sqrt{5}$,圆心到直线2x-y+m=0的距离d=$\frac{|m|}{\sqrt{4+1}}$=$\frac{|m|}{\sqrt{5}}$,
解:(1)∵圆x2+y2=5圆心为O(0,0),半径r=$\sqrt{5}$,圆心到直线2x-y+m=0的距离d=$\frac{|m|}{\sqrt{4+1}}$=$\frac{|m|}{\sqrt{5}}$,
∵直线与圆无公共点,∴d>r,即$\frac{|m|}{\sqrt{5}}$>$\sqrt{5}$,
∴m>5或m<-5.
故当m>5或m<-5时,直线与圆无公共点.
(2)如图所示,由平面几何垂径定理知
r2-d2=12,即5-$\frac{{m}^{2}}{5}$=1.
得m=±2$\sqrt{5}$,
∴当m=±2$\sqrt{5}$时,直线被圆截得的弦长为2.
点评 本题考查实数值的取值范围的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
14.下列各组函数中,f(x)与g(x)是同一函数的是( )
| A. | f(x)=x-1,g(x)=$\frac{{x}^{2}}{x}$-1 | B. | f(x)=x,g(x)=2${\;}^{lo{g}_{2}x}$ | ||
| C. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ |
15.在△ABC中,角A、B、C所对的边分别为a、b、c,|$\overrightarrow{AB}$|=5,20a$\overrightarrow{BC}$+15b$\overrightarrow{CA}$+12c$\overrightarrow{AB}$=$\overrightarrow{0}$,$\overrightarrow{BP}$=2$\overrightarrow{PA}$,则$\overrightarrow{CP}$$•\overrightarrow{AB}$的值为( )
| A. | $\frac{23}{3}$ | B. | -$\frac{7}{2}$ | C. | -$\frac{23}{3}$ | D. | -8 |
12.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+y≤3}\\{x+y≥2}\\{x≥0,y≥0}\end{array}\right.$,若z=-2x-y,则z的最小值为( )
| A. | -3 | B. | 3 | C. | -4 | D. | -6 |
16.已知正四棱锥的所有棱长都相等,那么该四棱锥的内切球与外接球的表面积之比为( )
| A. | $\frac{1}{4}$ | B. | $\frac{4}{9}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{2-\sqrt{3}}{2}$ |