题目内容
11.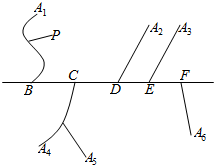 如图,一条公路的两侧有六个村庄,要建一个车站,要求到六个村庄的路程之和最小,应该选在哪里最合适?如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,那么这时车站设在什么地方好?
如图,一条公路的两侧有六个村庄,要建一个车站,要求到六个村庄的路程之和最小,应该选在哪里最合适?如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,那么这时车站设在什么地方好?
分析 由已知车站应设在B与F之间,车站不设在B、F间哪一点,A1与A6两村的人在公路上所走的路之和为B到F的路程,从而车站应设在C、E之间,不论车站设在C、E这段路之间的什么地方,A3和A4两村的人合起不一定要走C与E之间这段路,从而得到车站设在C或D与之间的任何地方都可以,如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,车站应该建立在D点.
解答  解:由题意,车站不能设在B点以西,否则每个村庄的人都必须多走B点以西这段路,
解:由题意,车站不能设在B点以西,否则每个村庄的人都必须多走B点以西这段路,
同理,车站也不能设在F点以东,
故车站应设在B与F之间,
车站不设在B、F间哪一点,A1与A6两村的人在公路上所走的路之和为常数,等于从B到F的路程,
既然A1和A6两村的人合在一起要走这样一段路,就可以不用考虑A1与A6,
故车站应设在C、E之间,
和前面一样,不论车站设在C、E这段路之间的什么地方,A3和A4两村的人合起不一定要走C与E之间这段路,
故可以去掉A3和A4,而只考虑A2和A5的人在C、D之间所走的这段路,
从上面的分析可以看出,车站设在C或D与之间的任何地方都可以,
同理,如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,车站应该建立在D点.
点评 本题考查车站应该建设有什么地方的确定,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
1.记$a=\frac{1}{e}-ln\frac{1}{e}$,$b=\frac{1}{2e}-ln\frac{1}{2e}$,$c=\frac{2}{e}-ln\frac{2}{e}$,其中e为自然对数的底数,则a,b,c这三个数的大小关系是( )
| A. | a>b>c | B. | a<b<c | C. | b>c>a | D. | b>a>c |
2.下列函数中,以$\frac{π}{2}$为最小正周期的奇函数是( )
| A. | y=sin2x+cos2x | B. | y=sin(4x+$\frac{π}{2}$) | C. | y=sin2xcos2x | D. | y=sin22x-cos22x |
16.已知正四棱锥的所有棱长都相等,那么该四棱锥的内切球与外接球的表面积之比为( )
| A. | $\frac{1}{4}$ | B. | $\frac{4}{9}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
3.函数y=-x2+2x+3(x≥0)的值域为( )
| A. | [3,+∞) | B. | (-∞,3] | C. | (-∞,4] | D. | [4,+∞) |