题目内容
5.已知实数a>0,且函数$f(x)=\frac{{{2^x}-a}}{{{2^x}+a}}$为奇函数.判断函数f(x)的单调性,并用单调性的定义证明.分析 根据题意,由于函数f(x)是定义在R上的奇函数,则有f(0)=0,代入数据,计算可得a的值,对f(x)的表达式变形,用作差法判断函数单调性即可.
解答 解:∵函数$f(x)=\frac{{{2^x}-a}}{{{2^x}+a}}$为奇函数,实数a>0,
∴有f(0)=0,即$\frac{1-a}{1+a}$=0,解可得a=1,∴f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$;
f(x)=1-$\frac{2}{{2}^{x}+1}$
理由:设x1<x2,
则f(x1)-f(x2)=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$,
∵x1<x2,∴f(x1)-f(x2)<0,
∴f(x)是增函数.
点评 本题考查函数的单调性、奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
11.cos$\frac{2017π}{6}$的值是( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
13.方程ex=2-x的解所在的一个区间为( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
14.直线y=5与y=-1在区间$[{0\;,\;\;\frac{4π}{ω}}]$上截曲线$y=msin\frac{ω}{2}x+n({m>0\;,\;\;n>0})$所得弦长相等且不为零,则下列描述正确的是( )
| A. | $m≤\frac{3}{2}\;,\;\;n=\frac{5}{2}$ | B. | m≤3,n=2 | C. | $m>\frac{3}{2}$ | D. | m>3,n=2 |
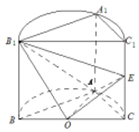 如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴截面)BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4
如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴截面)BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4