题目内容
17.已知函数$f(x)=\left\{\begin{array}{l}|{x+1}|\;,\;\;x≤-1\\ 2x\;,\;\;-1<x<2\\ x-1\;,\;\;x≥2\end{array}\right.$,则f[f(-2)]=2.分析 先求出f(-2)=|-2+1|=1,从而f[f(-2)]=f(1),由此能求出结果.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}|{x+1}|\;,\;\;x≤-1\\ 2x\;,\;\;-1<x<2\\ x-1\;,\;\;x≥2\end{array}\right.$,
∴f(-2)=|-2+1|=1,
f[f(-2)]=f(1)=2×1=2.
故答案为:2.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
12.若M{x|y=2x+1},N={y|y=-x2},则集合M,N的关系是( )
| A. | M∩N={(-1,1)} | B. | M∩N=∅ | C. | M⊆N | D. | N⊆M |
2.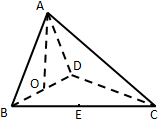 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{7}}{8}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\sqrt{2}$ |
6.将函数f(x)=$\sqrt{3}$sin2x-cos2x的图象向左平移φ(0<φ<$\frac{π}{2}$)个单位长度后得到函数y=g(x)的图象,若g(x)≤|g($\frac{π}{6}$)|对x∈R恒成立,则函数y=g(x)的单调递减区间是( )
| A. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | B. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | ||
| C. | [kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z) | D. | [kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$](k∈Z) |
7.已知正四面体棱长为4$\sqrt{2}$,则此正四面体外接球的表面积为( )
| A. | 36π | B. | 48π | C. | 64π | D. | 72π |
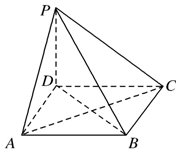 如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.
如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.