题目内容
14.直线y=5与y=-1在区间$[{0\;,\;\;\frac{4π}{ω}}]$上截曲线$y=msin\frac{ω}{2}x+n({m>0\;,\;\;n>0})$所得弦长相等且不为零,则下列描述正确的是( )| A. | $m≤\frac{3}{2}\;,\;\;n=\frac{5}{2}$ | B. | m≤3,n=2 | C. | $m>\frac{3}{2}$ | D. | m>3,n=2 |
分析 曲线$y=msin\frac{ω}{2}x+n({m>0\;,\;\;n>0})$的性质知,在一个周期上截直线y=5与y=-1所得的弦长相等且不为0,可知两条直线关于y=n对称,由此对称性可求出n,又截得的弦长不为0,故可得振幅大于 3.
解答 解:由题意可得$y=msin\frac{ω}{2}x+n({m>0\;,\;\;n>0})$的图象关于直线y=n对称,
因为曲线被直线y=5与y=-1所得的弦长相等,
所以直线y=5与直线y=-1关于y=n对称.
所以n=$\frac{5-1}{2}$=2,
又因为弦长相等且不为0,
所以振幅m>$\frac{5+1}{2}$=3.
故选D.
点评 本题考点y=Asin(ωx+φ)中参数的物理意义,考查三角函数的图象的性质及其与相应参数的关系,考查对三角函数图象的特征理解的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.设向量$\overrightarrow{a}$=(2tanα,tanβ),向量$\overrightarrow{b}$=(4,-3),且$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{0}$,则tan(α+β)等于( )
| A. | $\frac{1}{7}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{7}$ |
2.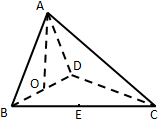 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{7}}{8}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\sqrt{2}$ |
19.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
6.将函数f(x)=$\sqrt{3}$sin2x-cos2x的图象向左平移φ(0<φ<$\frac{π}{2}$)个单位长度后得到函数y=g(x)的图象,若g(x)≤|g($\frac{π}{6}$)|对x∈R恒成立,则函数y=g(x)的单调递减区间是( )
| A. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | B. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | ||
| C. | [kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z) | D. | [kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$](k∈Z) |
3.在数列{an}中,a1=2,2an+1=2an+1,则a2015的值是( )
| A. | 1009 | B. | 1008 | C. | 1010 | D. | 1011 |
4.已知三条直线m,n,l,三个平面α,β,γ,下面说法正确的是( )
| A. | $\left.\begin{array}{l}{α⊥γ}\\{β⊥γ}\end{array}\right\}$⇒α∥β | B. | $\left.\begin{array}{l}{m⊥l}\\{n⊥l}\end{array}\right\}$⇒m∥n | C. | $\left.\begin{array}{l}{m∥β}\\{l⊥m}\end{array}\right\}$⇒l∥β | D. | $\left.\begin{array}{l}{m∥n}\\{n⊥γ}\end{array}\right\}$⇒m⊥γ |