题目内容
13.方程ex=2-x的解所在的一个区间为( )| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
分析 将x=-1,x=0,x=1代入方程转化为函数的表达式,结合零点的判定定理,得出答案.
解答 解:方程ex=2-x的解所在的一个区间就是函数f(x)=ex-2+x的零点所在区间.
∵f(-1)=$\frac{1}{e}$+1-2=$\frac{1}{e}$-1<0,f(0)=1-2=-1<0,
f(1)=e-1-2<0,f(2)=e2-4>0,
∴函数f(x)的零点在(1,2)内,
故选:D.
点评 本题考查了函数的零点的判定定理,是一道基础题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
4.设向量$\overrightarrow{a}$=(2tanα,tanβ),向量$\overrightarrow{b}$=(4,-3),且$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{0}$,则tan(α+β)等于( )
| A. | $\frac{1}{7}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{7}$ |
18.“a>b”是“a2>b2”的__________条件( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
2.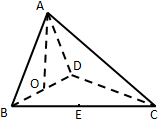 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
 如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )
如图,四面体ABCD中,O、E分别为BD、BC的中点,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,则异面直线AB与CD所成角的正切值为.( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{7}}{8}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\sqrt{2}$ |
3.在数列{an}中,a1=2,2an+1=2an+1,则a2015的值是( )
| A. | 1009 | B. | 1008 | C. | 1010 | D. | 1011 |
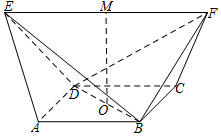 如图,在五面体ABCDEF中,底面ABCD是正方形,△ADE,△BCF都是等边三角形,EF∥AB,且EF>AB,M,O分别为EF,BD的中点,连接MO.
如图,在五面体ABCDEF中,底面ABCD是正方形,△ADE,△BCF都是等边三角形,EF∥AB,且EF>AB,M,O分别为EF,BD的中点,连接MO.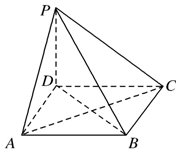 如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.
如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.