题目内容
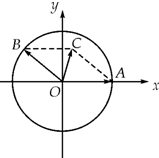如图，在xOy平面上，点A（1，0），点B在单位圆上，∠AOB=θ（0＜θ＜π）．（1）若点B（-
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 4 |
（2）若
| OA |
| OB |
| OC |
| OA |
| OC |
考点：任意角的三角函数的定义
专题：三角函数的求值
分析：（1）由题意利用任意角的三角函数的定义可得tanθ=
的值，可得tan2θ=
的值，进而求得tan（2θ+
）的值．
（2）由题意可得四边形OACB为菱形，求得Sθ+
•
=1×sin（π-θ）+
•(
+
)=1+
sin（θ+
），根据 0＜θ＜π，利用正弦函数的定义域和值域求得Sθ+
•
的取值范围．
| y |
| x |
| 2tanθ |
| 1-tan2θ |
| π |
| 4 |
（2）由题意可得四边形OACB为菱形，求得Sθ+
| OA |
| OC |
| OA |
| OA |
| OB |
| 2 |
| π |
| 4 |
| OA |
| OC |
解答：
解：（1）由题意可得tanθ=
=
=-
，
∴tan2θ=
=
．
∴tan（2θ+
）=
=-
．
（2）∵
+
=
，OA=OB，则四边形OACB为菱形，它的面积用Sθ表示，
则 Sθ+
•
=1×sin（π-θ）+
•(
+
)=sinθ+1+1×1×cosθ
=1+sinθ+cosθ=1+
sin（θ+
）．
∵0＜θ＜π，∴
＜θ+
＜
，
∴-
＜sin（θ+
）≤1，1+
sin（θ+
）∈（0，1+
]．
| y |
| x |
| ||
-
|
| 4 |
| 3 |
∴tan2θ=
| 2tanθ |
| 1-tan2θ |
| 24 |
| 7 |
∴tan（2θ+
| π |
| 4 |
| tan2θ+1 |
| 1-tan2θ×1 |
| 31 |
| 17 |
（2）∵
| OA |
| OB |
| OC |
则 Sθ+
| OA |
| OC |
| OA |
| OA |
| OB |
=1+sinθ+cosθ=1+
| 2 |
| π |
| 4 |
∵0＜θ＜π，∴
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴-
| ||
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
点评：本题主要考查任意角的三角函数的定义，两角和的正弦、正切公式，正弦函数的定义域和值域，属于中档题
练习册系列答案
相关题目
由曲线y=
，直线y=x，x=e所围成的封闭图形的面积S=（ ）
| 1 |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
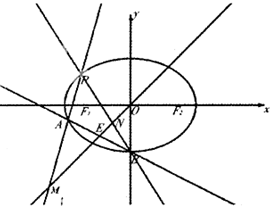已知椭圆C：