题目内容
由曲线y=
,直线y=x,x=e所围成的封闭图形的面积S=( )
| 1 |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:先联立两个曲线的方程,求出交点,以确定积分公式中x的取值范围,最后根据定积分的几何意义表示出区域的面积,根据定积分公式解之即可.
解答:
解:由曲线y=
,直线y=x,可得交点坐标为(1,1),
由曲线y=
,直线y=x,x=e所围成的封闭图形的面积S=
(x-
)dx=(
x2-lnx)
=
e2-1-
=
e2-
.
故选:B.
| 1 |
| x |
由曲线y=
| 1 |
| x |
| ∫ | e 1 |
| 1 |
| x |
| 1 |
| 2 |
| | | e 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选:B.
点评:本题主要考查了定积分在求面积中的应用,以及定积分的计算,属于基础题.

练习册系列答案
相关题目
某种程序如图所示,若该程序运行后输出的k的值是6,则满足条件的整数一共有( )个


| A、31 | B、32 | C、63 | D、64 |
已知命题p:lnx>0,命题q:ex>1,则命题p是命题q( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
在平行四边形ABCD中,
+
+
=( )
. |
| BC |
. |
| DC |
. |
| BA |
A、
| ||
B、
| ||
C、
| ||
D、
|
若向量
=(1,2),
=(4,5),则
=( )
| BA |
| CA |
| BC |
| A、(5,7) |
| B、(-3,-3) |
| C、(3,3) |
| D、(-5,-7) |
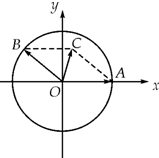 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).