题目内容
已知圆柱M的底面圆的半径与球O的半径相同,若圆柱M的高与球O直径相等,则它们的体积之比V圆柱:V球= (结果用数值作答).
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:设圆柱的高为h,底面圆半径为r,球的半径为R,分别求出圆柱和球的体积,代入可得答案.
解答:
解:设圆柱的高为h,底面圆半径为r,球的半径为R.
由题意,r=R,h=2R,
∴V圆柱=hπR2=2πR3,V球=
.
则V圆柱:V球=
故答案为:
由题意,r=R,h=2R,
∴V圆柱=hπR2=2πR3,V球=
| 4πR3 |
| 3 |
则V圆柱:V球=
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查的知识点旋转体的(圆柱、球)的体积,熟练掌握圆柱、球的体积公式是解答的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知a∈R,设p:a2+3a+2≤0;q:关于x的方程x2+2x+log2a=0有实数根.则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
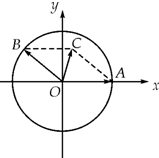 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).