题目内容
设正项数列{an}的前n项和为Sn,数列{Sn}的前n项积为Tn,且Sn+Tn=1.
(1)求a1,S2;
(2)求证:数列{
}是等差数列;
(3)试求数列{
}中最接近2012的项.
(1)求a1,S2;
(2)求证:数列{
| 1 |
| Tn |
(3)试求数列{
| 1 |
| an |
考点:数列递推式,等差关系的确定,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)根据条件建立方程组,即可求a1,S2;
(2)根据条件利用归纳推理得到Tn=
的通项公式,利用等差数列的定义即可证明数列{
}是等差数列;
(3)求出数列{
}的通项公式,即可得到结论.
(2)根据条件利用归纳推理得到Tn=
| 1 |
| n+1 |
| 1 |
| Tn |
(3)求出数列{
| 1 |
| an |
解答:
解:(1)当n=1时,a1+a1=2a1=1,解得a1=
,此时S1=
,T1=
.
当n=2时,S2+T2=1,即
+a2+
•(
+a2)=1,
解得a2=
,S2=
+
=
=
.
(2)当n=3时,a1+a2+a3=S3,S1S2S3+S3=1,
则a3=S3-S2=S3-
,T3=S1S2S3=
×
S3=
S3,
即T3+S3=
S3+S3=
S3=1,
即S3=
,则a3=
-
=
则a1=
,a2=
,a3=
…,
S1=
,S2=
,S3=
…,
T1=
,T2=
,T3=
…,
∴根据归纳推理可得
an=
,
Sn=
,
Tn=
,
∴
=n+1,
则
-
=n+1-n=1为常数,
∴数列{
}是等差数列.
(3)∵an=
,
∴
=n(n+1),
则当n=44时,44×45=1980,45×46=2070,
∴第44项最接近.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当n=2时,S2+T2=1,即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得a2=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 6 |
| 4 |
| 6 |
| 2 |
| 3 |
(2)当n=3时,a1+a2+a3=S3,S1S2S3+S3=1,
则a3=S3-S2=S3-
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
即T3+S3=
| 1 |
| 3 |
| 4 |
| 3 |
即S3=
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 12 |
则a1=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
S1=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
T1=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
∴根据归纳推理可得
an=
| 1 |
| n(n+1) |
Sn=
| n |
| n+1 |
Tn=
| 1 |
| n+1 |
∴
| 1 |
| Tn |
则
| 1 |
| Tn |
| 1 |
| Tn-1 |
∴数列{
| 1 |
| Tn |
(3)∵an=
| 1 |
| n(n+1) |
∴
| 1 |
| an |
则当n=44时,44×45=1980,45×46=2070,
∴第44项最接近.
点评:本题主要考查递推数列的应用,根据数列的递推关系,利用归纳推理是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
若向量
=(1,2),
=(4,5),则
=( )
| BA |
| CA |
| BC |
| A、(5,7) |
| B、(-3,-3) |
| C、(3,3) |
| D、(-5,-7) |
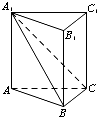 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.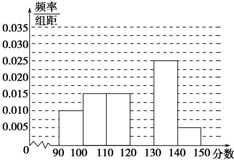 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题: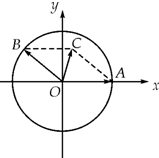 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).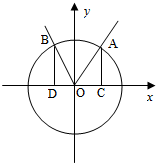 如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=
如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=