题目内容
9人成一排,规定甲、乙之间必须有四个人,问有多少种不同的排法?
考点:计数原理的应用
专题:排列组合
分析:先选4人排在甲乙之间,然后利用捆绑法,甲乙和已选的4人作为一个元素,和剩下的3人经行全排,问题得以解决.
解答:
解:第一步,排甲乙之间的4人有
种,第二步排甲乙有
种,第三步,甲乙和已选的4人作为一个元素,和剩下的3人经行全排
种,
根据分布计数原理得,
=40320种.
答:9人成一排,规定甲、乙之间必须有四个人,有40320种不同的排法.
| A | 4 7 |
| A | 2 2 |
| A | 4 4 |
根据分布计数原理得,
| A | 4 7 |
| •A | 2 2 |
| •A | 4 4 |
答:9人成一排,规定甲、乙之间必须有四个人,有40320种不同的排法.
点评:本题考查了排列问题的分步计数原理,并且利用捆绑法把甲乙和已选的4人作为一个元素,对于这类题要认真审题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
某种程序如图所示,若该程序运行后输出的k的值是6,则满足条件的整数一共有( )个


| A、31 | B、32 | C、63 | D、64 |
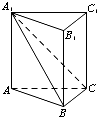 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,点M在线段AB上.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,点M在线段AB上.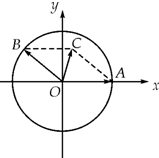 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).