题目内容
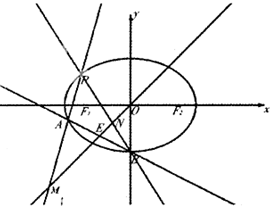 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)点B为椭圆C的下顶点,过点B的直线交椭圆C于另一点A(异于上顶点),且AB中点E在直线y=x上,
(ⅰ)求直线AB的方程;
(ⅱ)点P为椭圆C上异于A,B的任意一点,若直线AP,BP分别交直线y=x与M,N两点,证明:
| OM |
| ON |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据椭圆C:
+
=1(a>b>0)的长轴长为2
,离心率为
,求出a,b,即可求椭圆C的方程;
(2)(ⅰ)求出A的坐标,代入椭圆方程,即可求直线AB的方程;
(ⅱ)确定直线AP、BP的方程与y=x联立,求出M,N的坐标,利用向量的数量积公式,即可证明
•
为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
(2)(ⅰ)求出A的坐标,代入椭圆方程,即可求直线AB的方程;
(ⅱ)确定直线AP、BP的方程与y=x联立,求出M,N的坐标,利用向量的数量积公式,即可证明
| OM |
| ON |
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)的长轴长为2
,离心率为
,
∴2a=2
,e=
=
,
∴a=
,b=1,
∴椭圆C的方程为
+y2=1…(3分)
(2)(i)解:由(1)知B(0,-1),设点E(m,m).
∵点E为AB中点,∴A(2m,2m+1),
又∵点A在椭圆上,∴
+(2m+1)2=1
解得:m=0(舍)或m=-
,
∴直线AB的方程为:y=-
x-1.…(8分)
(ii)证明:∵点M、N在y=x上,∴设M(x1,x1),N(x2,x2),P(x0,y0),∴
+y02=1,
∵A(-
,-
),∴直线AP的方程为:(y+
)(x0+
)=(y0+
)(x+
),
与y=x联立得x1=
•
,
同理:直线BP的方程为:(y+1)x0=(y0+1)x
与y=x联立得x2=
,…(10分)
∴
•
=(x1,x1)•(x2,x2)=2x1x2=
•
=
•
=
•
=
•
=
,
∴
•
为定值. …(12分)
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
∴2a=2
| 2 |
| c |
| a |
| ||
| 2 |
∴a=
| 2 |
∴椭圆C的方程为
| x2 |
| 2 |
(2)(i)解:由(1)知B(0,-1),设点E(m,m).
∵点E为AB中点,∴A(2m,2m+1),
又∵点A在椭圆上,∴
| (2m)2 |
| 2 |
解得:m=0(舍)或m=-
| 2 |
| 3 |
∴直线AB的方程为:y=-
| 1 |
| 2 |
(ii)证明:∵点M、N在y=x上,∴设M(x1,x1),N(x2,x2),P(x0,y0),∴
| x02 |
| 2 |
∵A(-
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
与y=x联立得x1=
| 1 |
| 3 |
| x0-4y0 |
| y0-x0-1 |
同理:直线BP的方程为:(y+1)x0=(y0+1)x
与y=x联立得x2=
| x0 |
| y0-x0+1 |
∴
| OM |
| ON |
| 2 |
| 3 |
| x02-4x0y0 |
| (y0-x0+1)•(y0-x0-1) |
| 2 |
| 3 |
| x02-4x0y0 |
| (y0-x0)2-1 |
=
| 2 |
| 3 |
| x02-4x0y0 |
| y02-2x0y0+x02-1 |
| 2 |
| 3 |
| x02-4x0y0 | ||
1-
|
| 4 |
| 3 |
∴
| OM |
| ON |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量的数量积公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知命题p:lnx>0,命题q:ex>1,则命题p是命题q( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
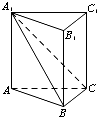 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,点M在线段AB上.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,点M在线段AB上.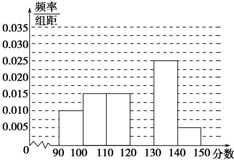 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题: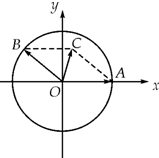 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).