题目内容
已知抛物线C:y2=2px(p>0)的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且|MN|=8.
(1)求抛物线C的方程;
(2)设直线l为抛物线C的切线,且l∥MN,P为l上一点,求
•
的最小值.
(1)求抛物线C的方程;
(2)设直线l为抛物线C的切线,且l∥MN,P为l上一点,求
| PM |
| PN |
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)过点F且斜率为1的直线代入抛物线,利用|MN|=8,可得x1+x2+p=8,即可求抛物线C的方程;
(2)设l方程为y=x+b,代入y2=4x,利用直线l为抛物线C的切线,求出b,再利用向量的数量积公式求
•
,利用配方法可求最小值.
(2)设l方程为y=x+b,代入y2=4x,利用直线l为抛物线C的切线,求出b,再利用向量的数量积公式求
| PM |
| PN |
解答:
 解:(1)由题可知F(
解:(1)由题可知F(
,0),则该直线方程为:y=x-
,…(1分)
代入y2=2px(p>0)得:x2-3px+
=0,
设M(x1,y1),N(x2,y2),则有x1+x2=3p…(3分)
∵|MN|=8,∴x1+x2+p=8,即3p+p=8,解得p=2
∴抛物线的方程为:y2=4x.…(5分)
(2)设l方程为y=x+b,代入y2=4x,得x2+(2b-4)x+b2=0,
∵l为抛物线C的切线,∴△=0,
解得b=1,∴l:y=x+1…(7分)
由(1)可知:x1+x2=6,x1x2=1
设P(m,m+1),则
=(x1-m,y1-(m+1)),
=(x2-m,y2-(m+1))
∴
•
=(x1-m)(x2-m)+[y1-(m+1)][y2-(m+1)]
=x1x2-m(x1+x2)+m2+y1y2-(m+1)(y1+y2)+(m+1)2
∵x1+x2=6,x1x2=1,(y1y2)2=16x1x2=16,y1y2=-4,y12-y22=4(x1-x2),
∴y1+y2=4
=4,
∴
•
=1-6m+m2-4-4(m+1)+(m+1)2…(10分)
=2[m2-4m-3]=2[(m-2)2-7]≥-14
当且仅当m=2时,即点P的坐标为(2,3)时,
•
的最小值为-14.…(12分)
 解:(1)由题可知F(
解:(1)由题可知F(| p |
| 2 |
| p |
| 2 |
代入y2=2px(p>0)得:x2-3px+
| p2 |
| 4 |
设M(x1,y1),N(x2,y2),则有x1+x2=3p…(3分)
∵|MN|=8,∴x1+x2+p=8,即3p+p=8,解得p=2
∴抛物线的方程为:y2=4x.…(5分)
(2)设l方程为y=x+b,代入y2=4x,得x2+(2b-4)x+b2=0,
∵l为抛物线C的切线,∴△=0,
解得b=1,∴l:y=x+1…(7分)
由(1)可知:x1+x2=6,x1x2=1
设P(m,m+1),则
| PM |
| PN |
∴
| PM |
| PN |
=x1x2-m(x1+x2)+m2+y1y2-(m+1)(y1+y2)+(m+1)2
∵x1+x2=6,x1x2=1,(y1y2)2=16x1x2=16,y1y2=-4,y12-y22=4(x1-x2),
∴y1+y2=4
| x1-x2 |
| y1-y2 |
∴
| PM |
| PN |
=2[m2-4m-3]=2[(m-2)2-7]≥-14
当且仅当m=2时,即点P的坐标为(2,3)时,
| PM |
| PN |
点评:本题考查抛物线方程,直线与抛物线的位置关系,考查抛物线的定义,韦达定理的运用,考查向量的数量积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
在平行四边形ABCD中,
+
+
=( )
. |
| BC |
. |
| DC |
. |
| BA |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,点M在线段AB上.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,点M在线段AB上.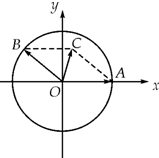 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).