题目内容
已知数列{an},满足a1=4,an+1=5nan,求数列{an}通项公式.
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由数列递推式得到
=5n,分别取n=1,2,…,n-1得到n-1个等式,累积后借助于等差数列的通项公式得答案.
| an+1 |
| an |
解答:
解:由an+1=5nan,得
=5n.
=51,
=52,
=53,
…
=5n-1(n≥2),
累积得:
=51+2+…+(n-1)=5
,
∴an=a1•5
.
又a1=4,
∴an=4•5
.
| an+1 |
| an |
| a2 |
| a1 |
| a3 |
| a2 |
| a4 |
| a3 |
…
| an |
| an-1 |
累积得:
| an |
| a1 |
| n(n-1) |
| 2 |
∴an=a1•5
| n(n-1) |
| 2 |
又a1=4,
∴an=4•5
| n(n-1) |
| 2 |
点评:本题考查数列递推式,考查了累积法求数列的通项公式,训练了等差数列前n项和公式的用法,是中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
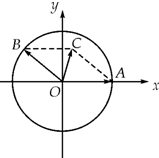 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).