题目内容
下列命题:
①数列{an}为递减的等差数列且a1+a5=0,设数列{an}的前n项和为Sn,则当n=4时,Sn取得最大值;
②设函数f(x)=x2+bx+c,则x0满足关于方程2x+b=0的充要条件是对任意x∈R均有f(x)≥f(x0);
③在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,直线BC1与平面BB1D1D所成角的正弦值为
;
④定义在R上的函数y=f(x)满足f(5+x)=f(-x)且(x-
)f/(x)>0,已知x1<x2,则f(x1)>f(x2)是x1+x2<5的充要条件.
其中正确命题的序号是 (把所有正确命题的序号都写上).
①数列{an}为递减的等差数列且a1+a5=0,设数列{an}的前n项和为Sn,则当n=4时,Sn取得最大值;
②设函数f(x)=x2+bx+c,则x0满足关于方程2x+b=0的充要条件是对任意x∈R均有f(x)≥f(x0);
③在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,直线BC1与平面BB1D1D所成角的正弦值为
| ||
| 5 |
④定义在R上的函数y=f(x)满足f(5+x)=f(-x)且(x-
| 5 |
| 2 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:根据等差数列的性质、数列的单调性判断出①不正确;根据二次函数的性质判断出②正确;由题意和线面角的定义判断出③正确;由函数的对称性、导数与函数的单调性的关系判断出④正确.
解答:
解:对①,由等差数列的性质和a1+a5=2a3=0,得a3=0,
又数列{an}单调递减,所以当n=2或n=3时,Sn取得最大值,则①不正确;
对②,当x0=-
时,函数f(x)=x2+bx+c取最小值,即f(x)≥f(-
),
由2x+b=0得,x=-
,即x0=-
,故条件充分,
反之也成立,故必要,则②正确;
对③,于连结A1C1,设A1C1∩B1D1=O,连结OB
由已知得C1O⊥面BB1D1D,∴∠C1BO为所求角,
在Rt△C1OB中,得sin∠C1BO=
,③正确;
对④,∵f(5+x)=f(-x),所以函数f(x)关于x=
对称
∵(x-
)f′(x)>0,
∴x>
时,f′(x)>0,函数f(x)单调递增;
当x<
时,f'(x)<0,函数f(x)单调递减;
当x1<x2时,若f(x1)>f(x2)则有x1<x2<5-x1,∴x1+x2<5成立,故条件充分,
当x1+x2<5时,必有x2<5-x1成立,又因为x1<x2,所以f(x1)>f(x2)成立,故必要,
f(x1)>f(x2)是x1+x2<5的充要条件,则④正确,
故答案为:②③④.
又数列{an}单调递减,所以当n=2或n=3时,Sn取得最大值,则①不正确;
对②,当x0=-
| b |
| 2 |
| b |
| 2 |
由2x+b=0得,x=-
| b |
| 2 |
| b |
| 2 |
反之也成立,故必要,则②正确;
对③,于连结A1C1,设A1C1∩B1D1=O,连结OB

由已知得C1O⊥面BB1D1D,∴∠C1BO为所求角,
在Rt△C1OB中,得sin∠C1BO=
| ||
| 5 |
对④,∵f(5+x)=f(-x),所以函数f(x)关于x=
| 5 |
| 2 |
∵(x-
| 5 |
| 2 |
∴x>
| 5 |
| 2 |
当x<
| 5 |
| 2 |
当x1<x2时,若f(x1)>f(x2)则有x1<x2<5-x1,∴x1+x2<5成立,故条件充分,
当x1+x2<5时,必有x2<5-x1成立,又因为x1<x2,所以f(x1)>f(x2)成立,故必要,
f(x1)>f(x2)是x1+x2<5的充要条件,则④正确,
故答案为:②③④.
点评:本题考查了命题的真假性判断,充要性的判断,涉及的知识点多,综合性强,难度大.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
记a=log2
,b=70.3.c=(
)9.1,则a、b、c的大小关系是( )
| 5 |
| 6 |
| 1 |
| 7 |
| A、a<b<c |
| B、c<b<a |
| C、a<c<b |
| D、b<a<c |
函数f(x)=
的定义域区间为( )
log
|
A、[1,
| ||
B、[1,
| ||
C、(-∞,
| ||
D、(1,
|
如图是正方体ABCD-A′B′C′D′中,异面直线A′D与CD′所成的角是( )
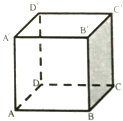

| A、30° | B、45° |
| C、60° | D、90° |
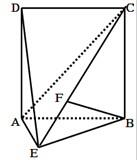 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE,求DE与平面AEC所成夹角的正弦值.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE,求DE与平面AEC所成夹角的正弦值.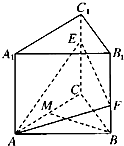 如图,直三棱柱ABC-A1B1C1中,CC1=3,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB.
如图,直三棱柱ABC-A1B1C1中,CC1=3,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB.