题目内容
已知函数f(x)是定义在R上的奇函数,且当x≥0时有f(x)=
.
(1)判断函数f(x)的单调性,并求使不等式f(2m+1)+f(m2-2m-4)>0成立的实数m的取值范围.
(2)若a、b、c分别是△ABC的三个内角A、B、C所对的边,△ABC面积S△ABC=
,c=f(4),A=60°,求a、b的值.
| 4x |
| x+4 |
(1)判断函数f(x)的单调性,并求使不等式f(2m+1)+f(m2-2m-4)>0成立的实数m的取值范围.
(2)若a、b、c分别是△ABC的三个内角A、B、C所对的边,△ABC面积S△ABC=
| ||
| 2 |
考点:余弦定理,函数单调性的判断与证明,函数奇偶性的性质
专题:解三角形
分析:(1)首先根据函数的单调性判断函数的单调性,然后列出不等式即可求出m的取值范围;
(2)根据三角形的面积求出b的值,再由余弦定理求出a的值.
(2)根据三角形的面积求出b的值,再由余弦定理求出a的值.
解答:
解:(1)∵当x≥0时,f(x)时有f(x)=
=4-
∴f(x)在[0,+∞)上是增函数,
又∵f(x)是奇函数,
∴f(x)在(-∞,+∞)是增函数,
∵f(2m+1)+f(m2-2m-4)>0
∴2m+1>-(m2-2m-4)
∴m<-
或m>
(2)c=f(4)=2,
∵S△ABC=
bcsinA
,∴
b•2sin60°=
,得b=1.
由余弦定理得:a2=b2+c2-2bccosA=12+22-2×1×2•cos60°=3,所以a=
.
| 4x |
| x+4 |
| 16 |
| x+4 |
∴f(x)在[0,+∞)上是增函数,
又∵f(x)是奇函数,
∴f(x)在(-∞,+∞)是增函数,
∵f(2m+1)+f(m2-2m-4)>0
∴2m+1>-(m2-2m-4)
∴m<-
| 3 |
| 3 |
(2)c=f(4)=2,
∵S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
由余弦定理得:a2=b2+c2-2bccosA=12+22-2×1×2•cos60°=3,所以a=
| 3 |
点评:本题考查余弦定理、三角形的面积公式以及函数的单调性、奇偶性的综合应用,是一道中档题.

练习册系列答案
相关题目
已知集合A={x|-3≤x<4},B={x|-2≤x≤5},则A∩B=( )
| A、{x|-3≤x≤5} |
| B、{x|-3≤x<4} |
| C、{x|-2≤x≤5} |
| D、{x|-2≤x<4} |
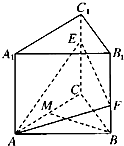 如图,直三棱柱ABC-A1B1C1中,CC1=3,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB.
如图,直三棱柱ABC-A1B1C1中,CC1=3,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB.