题目内容
已知抛物线y2=4x,焦点为F,点A(-3,0).
(1)过点A的直线与抛物线只有一个交点的直线有几条,并写出直线方程;
(2)过焦点的直线l与抛物线相交于B、C两点,且
=2
,求l的方程.
(1)过点A的直线与抛物线只有一个交点的直线有几条,并写出直线方程;
(2)过焦点的直线l与抛物线相交于B、C两点,且
| BF |
| FC |
考点:直线与圆锥曲线的关系
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)当过点A的直线经过F,则与抛物线只有一个交点;当过点A的直线与抛物线相切,则与抛物线只有一个交点,设方程为:y=k(x+3),联立抛物线方程,消去y,由判别式为0,解出k即可得到直线方程;
(2)设过焦点的直线l:y=k(x-1),联立抛物线方程,消去y,运用韦达定理,判别式大于0,再由向量的坐标运算,得到方程,消去x1,x2得到k的方程,解出k,检验即可得到直线方程.
(2)设过焦点的直线l:y=k(x-1),联立抛物线方程,消去y,运用韦达定理,判别式大于0,再由向量的坐标运算,得到方程,消去x1,x2得到k的方程,解出k,检验即可得到直线方程.
解答:
解:(1)当过点A的直线经过F,则与抛物线只有一个交点,方程为y=0.
当过点A的直线与抛物线相切,则与抛物线只有一个交点,
设方程为:y=k(x+3),联立抛物线方程,消去y,
得到:k2x2+(6k2-4)x+9k2=0,
由△=0,即(6k2-4)2-36k4=0,解得,k=±
.
故所求直线有3条,方程为:x=0,或y=±
(x+3);
(2)设过焦点的直线l:y=k(x-1),
联立抛物线方程,消去y,得到k2x2-(2k2+4)x+k2=0,
设B(x1,y1)、C(x2,y2),
则△=(2k2+4)2-4k4>0①
x1+x2=
,x1x2=1,
又
=2
,则1-x1=2(x2-1),
则消去x1,x2得到k的方程:(k2-4)(k2+8)=k4,
解得,k2=8,即有k=±2
.
代入①检验成立,
则直线l的方程为:y=±2
(x-1).
当过点A的直线与抛物线相切,则与抛物线只有一个交点,
设方程为:y=k(x+3),联立抛物线方程,消去y,
得到:k2x2+(6k2-4)x+9k2=0,
由△=0,即(6k2-4)2-36k4=0,解得,k=±
| ||
| 3 |
故所求直线有3条,方程为:x=0,或y=±
| ||
| 3 |
(2)设过焦点的直线l:y=k(x-1),
联立抛物线方程,消去y,得到k2x2-(2k2+4)x+k2=0,
设B(x1,y1)、C(x2,y2),
则△=(2k2+4)2-4k4>0①
x1+x2=
| 2k2+4 |
| k2 |
又
| BF |
| FC |
则消去x1,x2得到k的方程:(k2-4)(k2+8)=k4,
解得,k2=8,即有k=±2
| 2 |
代入①检验成立,
则直线l的方程为:y=±2
| 2 |
点评:本题考查抛物线方程及运用,考查直线与抛物线的位置关系,考查联立直线方程和抛物线方程,消去未知数,运用韦达定理,以及向量的运算,考查运算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=
的定义域区间为( )
log
|
A、[1,
| ||
B、[1,
| ||
C、(-∞,
| ||
D、(1,
|
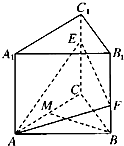 如图,直三棱柱ABC-A1B1C1中,CC1=3,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB.
如图,直三棱柱ABC-A1B1C1中,CC1=3,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB.