题目内容
若-1＜sinA＜0.5，则∠A的取值范围为 ．
考点：三角函数线
专题：三角函数的图像与性质
分析：在单位圆中作出满足sinx=-1和sinx=0.5的角的正弦线，观察得到在一个周期内满足弦线大于-1，小于0.5的角的范围，由此结合终边相同的角的集合，即可得到满足条件A的范围．
解答：
解：解：如图，作出满足sinx=0.5的角的正弦线M1P1和M2P2，
可得∠M20P2=
，∠M10P1=
，
当角的终边位于图中阴影部分时，正弦线小于0.5，其中x=-
时的正弦线为-1，
所以满足-1＜sinA＜0.5的A的范围是{x|2kπ+
＜A＜2kπ+
并且A≠2kπ-
}（k∈Z）；
故答案为：{x|2kπ+
＜A＜2kπ+
并且A≠2kπ-
}（k∈Z）；
可得∠M20P2=
| π |
| 6 |
| 5π |
| 6 |
当角的终边位于图中阴影部分时，正弦线小于0.5，其中x=-
| π |
| 2 |
所以满足-1＜sinA＜0.5的A的范围是{x|2kπ+
| 5π |
| 6 |
| 13π |
| 6 |
| π |
| 2 |
故答案为：{x|2kπ+
| 5π |
| 6 |
| 13π |
| 6 |
| π |
| 2 |
点评：本题求满足条-1＜sinA＜0.5的解集．着重考查了终边相同的角的集合、三角函数的定义与三角函数线的作法等知识．
练习册系列答案
相关题目
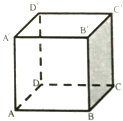
如图是正方体ABCD-A′B′C′D′中，异面直线A′D与CD′所成的角是（ ）
| A、30° | B、45° |
| C、60° | D、90° |
命题p：在区间[1，+∞）上至少有一个x0，使得x03-x0-1＞0，则￢p为（ ）
| A、?x∈[1，+∞），x3-x-1≤0 |
| B、?x∈（-∞，1]，x3-x-1≤0 |
| C、?x0∈[1，+∞），x03-x0-1≤0 |
| D、?x0∈（-∞，1]，x03-x0-1≤0 |
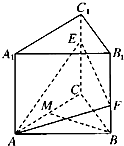如图，直三棱柱ABC-A1B1C1中，CC1=3，底面是边长为2的正三角形，点E，F分别是棱CC1，BB1上的点，点M是线段AC上的动点，EC=2FB．已知Sn=
+
+
+…+
，则当a=2时，S6=（ ）
| 1 |
| a |
| 2 |
| a2 |
| 3 |
| a3 |
| n |
| an |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
已知集合A={x|-3≤x＜4}，B={x|-2≤x≤5}，则A∩B=（ ）
| A、{x|-3≤x≤5} |
| B、{x|-3≤x＜4} |
| C、{x|-2≤x≤5} |
| D、{x|-2≤x＜4} |