题目内容
已知函数f(x)=
+x.
(1)判断函数f(x)的奇偶性,并证明;
(2)用函数单调性的定义证明:f(x)在区间(0,2)上是减函数.
| 4 |
| x |
(1)判断函数f(x)的奇偶性,并证明;
(2)用函数单调性的定义证明:f(x)在区间(0,2)上是减函数.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)函数f(x)是奇函数.运用定义,求出定义域,再计算f(-x),与f(x)比较,即可得到奇偶性;
(2)运用单调性的定义证明,注意取值、作差、变形、定符号、下结论几个步骤.
(2)运用单调性的定义证明,注意取值、作差、变形、定符号、下结论几个步骤.
解答:
解:(1)函数f(x)是奇函数.
证明:定义域为{x|x≠0}关于原点对称,
且f(-x)=-x-
=-(x+
)=-f(x),
则f(-x)=-f(x),
故f(x)是奇函数;
(2)证明:设m,n是(0,2)上的两个任意实数,且m<n,
f (n)-f (m)=
+n-(
+m)
=
,由于m,n∈(0,2)且m<n,则n-m>0,mn-4<0
则f(n)-f(m)<0,
则f(x)在区间(0,2)上是减函数.
证明:定义域为{x|x≠0}关于原点对称,
且f(-x)=-x-
| 4 |
| x |
| 4 |
| x |
则f(-x)=-f(x),
故f(x)是奇函数;
(2)证明:设m,n是(0,2)上的两个任意实数,且m<n,
f (n)-f (m)=
| 4 |
| n |
| 4 |
| m |
=
| (n-m)(mn-4) |
| mn |
则f(n)-f(m)<0,
则f(x)在区间(0,2)上是减函数.
点评:本题考查函数的奇偶性的判断,考查函数的单调性的证明,注意运用定义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a,b是正实数,A是a,b的等差中项,G是a,b等比中项,则( )
| A、ab≤AG |
| B、ab≥AG |
| C、ab≤|AG| |
| D、ab>AG |
记a=log2
,b=70.3.c=(
)9.1,则a、b、c的大小关系是( )
| 5 |
| 6 |
| 1 |
| 7 |
| A、a<b<c |
| B、c<b<a |
| C、a<c<b |
| D、b<a<c |
函数f(x)=
的定义域区间为( )
log
|
A、[1,
| ||
B、[1,
| ||
C、(-∞,
| ||
D、(1,
|
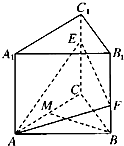 如图,直三棱柱ABC-A1B1C1中,CC1=3,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB.
如图,直三棱柱ABC-A1B1C1中,CC1=3,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB.