题目内容
设函数f(x)=sin(ωx-
)-2cos2
x+1(ω>0).直线y=
与函数y=f(x)图象相邻两交点的距离为π.
(Ⅰ)求ω的值;
(Ⅱ)在△ABC中,角A、B、C所对的边分别是a、b、c,若点(
,0)是函数y=f(x)图象的一个对称中心,且b=3,求△ABC周长的取值范围.
| π |
| 6 |
| ω |
| 2 |
| 3 |
(Ⅰ)求ω的值;
(Ⅱ)在△ABC中,角A、B、C所对的边分别是a、b、c,若点(
| B |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(Ⅰ)利用三角恒等变换化f(x)为Asin(ωx+φ)的形式,在由题意得到函数的周期,由周期公式求得ω的值;
(Ⅱ)把(Ⅰ)中求得的ω值代入函数解析式,由点(
,0)是函数y=f(x)图象的一个对称中心求得B,利用正弦定理求出△ABC的外接圆的直径,把△ABC的周长用含有角A的代数式表示,则△ABC周长的取值范围可求.
(Ⅱ)把(Ⅰ)中求得的ω值代入函数解析式,由点(
| B |
| 2 |
解答:
解:(Ⅰ)f(x)=sin(ωx-
)-2cos2
x+1
=sinωx•cos
-cosωx•sin
-2•
+1
=
sinωx-
cosωx=
(
sinωx-
cosωx)
=
sin(ωx-
).
∵函数f(x)的最大值为
,以题意,函数f(x)的最小正周期为π,
由
=π,得ω=2;
(Ⅱ)∵f(x)=
sin(2x-
),依题意
sin(B-
)=0,
sin(B-
)=0.
∵0<B<π,-
<B-
<
π,
∴B-
=0,B=
,
则2R=
=
=
=2
,
∴△ABC周长为a+b+c=3+2
(sinA+sinC)=3+6sin(A+
)(0<A<
π)∈(6,9].
| π |
| 6 |
| ω |
| 2 |
=sinωx•cos
| π |
| 6 |
| π |
| 6 |
| 1+cosωx |
| 2 |
=
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| 3 |
| π |
| 3 |
∵函数f(x)的最大值为
| 3 |
由
| 2π |
| ω |
(Ⅱ)∵f(x)=
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
sin(B-
| π |
| 3 |
∵0<B<π,-
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
∴B-
| π |
| 3 |
| π |
| 3 |
则2R=
| b |
| sinB |
| 3 | ||
sin
|
| 3 | ||||
|
| 3 |
∴△ABC周长为a+b+c=3+2
| 3 |
| π |
| 6 |
| 2 |
| 3 |
点评:本题考查了三角函数中的恒等变换应用,考查了y=Asin(ωx+φ)型的函数的图象和性质,训练了正弦定理在解题中的应用,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
以下有关命题的说法错误的是( )
| A、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | ||||||
B、“cosα=-
| ||||||
| C、对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0 | ||||||
| D、若p∧q为假命题,则p、q均为假命题 | ||||||
| E、对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0 |
在平面直角坐标系中,x轴的正半轴上有4个点,y轴的正半轴上有5个点,这9个点任意两点连线,则所有连线段的交点落入第一象限的个数最多是( )
| A、30 | B、60 |
| C、120 | D、240 |
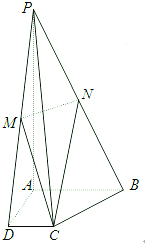 如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
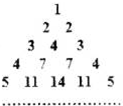 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn.
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn.