题目内容
已知椭圆E:
+
=1(a>b>0)的离心率为
,且过点(
,
).
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线l:y=kx+t 与圆C:x2+y2=R2(1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
①求证:k2=
;
②当R为何值时,丨AB丨取得最大值?并求出最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线l:y=kx+t 与圆C:x2+y2=R2(1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
①求证:k2=
| R2-1 |
| 4-R2 |
②当R为何值时,丨AB丨取得最大值?并求出最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(I)由椭圆E:
+
=1(a>b>0)的离心率为
,且过点(
,
),建立方程组,求出a,b,即可求椭圆E的方程;
(Ⅱ)①由题意可设直线l的方程为y=kx+t,由直线l与圆O相切可得r,t与k的关系式,然后联立直线与椭圆方程,由直线与椭圆C只有一个公共点可得k,t的关系,即可得证;
②结合方程的根与系数关系及由直角三角形OAB中,|AB|2=|OB|2-|OA|2,利用基本不等式即可求解最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
(Ⅱ)①由题意可设直线l的方程为y=kx+t,由直线l与圆O相切可得r,t与k的关系式,然后联立直线与椭圆方程,由直线与椭圆C只有一个公共点可得k,t的关系,即可得证;
②结合方程的根与系数关系及由直角三角形OAB中,|AB|2=|OB|2-|OA|2,利用基本不等式即可求解最大值.
解答:
解:(Ⅰ)∵椭圆E:
+
=1(a>b>0)的离心率为
,且过点(
,
),
∴
,
∴a=2,b=1,
∴椭圆E的方程为
+y2=1…(4分)
(Ⅱ) 证明:①由直线l与圆C:x2+y2=R2(1<R<2)相切于A,得R=
,
即 t2=R2(1+k2)…(5分)
又∵l与椭圆E只有一个公共点B,
由
得(1+4k2)x2+8ktx+4t2-4=0,
∵直线与椭圆C只有一个公共点
∴△=(8kt)2-4(+4k2)(4t2-4)=0
∴t2=1+4k2②
由①②,得k2=
…(8分)
②解:设B(x0,y0),由k2=
得t2=
由韦达定理,x02=
∵B(x0,y0)点在椭圆上,
∴y02=1-
x02=
∴|OB|2=x02+y02=5-
,…(10分)
在直角三角形OAB中,|AB|2=|OB|2-|OA|2=5-(
+R2),
∵
+R2≥4,当且仅当R=
∈(1,2)时取等号,
∴|AB|2≤5-4=1,
∴AB的最大值为1.…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴
|
∴a=2,b=1,
∴椭圆E的方程为
| x2 |
| 4 |
(Ⅱ) 证明:①由直线l与圆C:x2+y2=R2(1<R<2)相切于A,得R=
| |t| | ||
|
即 t2=R2(1+k2)…(5分)
又∵l与椭圆E只有一个公共点B,
由
|
∵直线与椭圆C只有一个公共点
∴△=(8kt)2-4(+4k2)(4t2-4)=0
∴t2=1+4k2②
由①②,得k2=
| R2-1 |
| 4-R2 |
②解:设B(x0,y0),由k2=
| R2-1 |
| 4-R2 |
| 3R2 |
| 4-R2 |
由韦达定理,x02=
| 16R2-16 |
| 3R2 |
∵B(x0,y0)点在椭圆上,
∴y02=1-
| 1 |
| 4 |
| 4-R2 |
| 3R2 |
∴|OB|2=x02+y02=5-
| 4 |
| R2 |
在直角三角形OAB中,|AB|2=|OB|2-|OA|2=5-(
| 4 |
| R2 |
∵
| 4 |
| R2 |
| 2 |
∴|AB|2≤5-4=1,
∴AB的最大值为1.…(12分)
点评:本题主要考查了利用椭圆的性质求解椭圆方程,直线与椭圆相交关系、相切关系的应用及方程的根与系数关系的应用,本题具有一定的综合性.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
动点P在函数y=sin2x的图象上移动,动点Q(x,y)满足
=(
,0),则动点Q的轨迹方程为( )
| PQ |
| π |
| 8 |
A、y=sin(2x+
| ||
B、y=sin(2x-
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
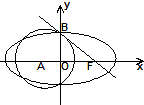 如图,已知点F为椭圆C:
如图,已知点F为椭圆C: 已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.