��Ŀ����
 �ò�����Ȼ��������ͼ����������aij��i��j����ʾ��i�е�j������i��j��N+����ʹ��ai1=aij=i��ÿ���е����������ֱ�����䡰����ϵ�������֮�ͣ����n��n��N+�����еĸ���֮��Ϊbn��
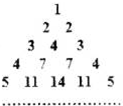
�ò�����Ȼ��������ͼ����������aij��i��j����ʾ��i�е�j������i��j��N+����ʹ��ai1=aij=i��ÿ���е����������ֱ�����䡰����ϵ�������֮�ͣ����n��n��N+�����еĸ���֮��Ϊbn����1��д��b1��b2��b3��b4����д��bn+1��bn�ĵ��ƹ�ϵ����Ҫ��֤������
��2����cn=bn+2��֤��{cn}�ǵȱ����У������{bn}��ͨ�ʽ��
��3������{bn}���Ƿ���ڲ�ͬ������bp��bq��br��p��q��r��N+��ǡ�óɵȲ����У������ڣ����p��q��r�Ĺ�ϵ���������ڣ�˵�����ɣ�
���㣺���е�Ӧ��
ר�⣺
��������1����������������b1��b2��b3��b4������bn+1=a��n+1��1+a��n+1��2+��+a��n+1����n+1��=2��an1+an2+��+ann��+2=2bn+2��
��2����bn+1=2bn+2���ɵ�bn+1+2=2��bn+2�����Ӷ�{bn+2}����b1+2=3Ϊ���2Ϊ���ȵĵȱ����У��������{bn}��ͨ�ʽ��
��3����p��q��r��{bn}�ǵ������У�2bq=bp+br���ɴ��ܵ�������{bn}�в����ڲ�ͬ������bp��bq��brǡ�óɵȲ����У�
��2����bn+1=2bn+2���ɵ�bn+1+2=2��bn+2�����Ӷ�{bn+2}����b1+2=3Ϊ���2Ϊ���ȵĵȱ����У��������{bn}��ͨ�ʽ��
��3����p��q��r��{bn}�ǵ������У�2bq=bp+br���ɴ��ܵ�������{bn}�в����ڲ�ͬ������bp��bq��brǡ�óɵȲ����У�
���
��1���⣺b1=1��b2=2+2=4��b3=3+4+3=10��b4=4+7+7+4=22��
bn+1=a��n+1��1+a��n+1��2+��+a��n+1����n+1��=n+1+��an1+an2��+��+��an��n-1��ann��+n+1=2��an1+an2+��+ann��+2=2bn+2��
��2��֤������bn+1=2bn+2��
��bn+1+2=2��bn+2��
��{bn+2}����b1+2=3Ϊ���2Ϊ���ȵĵȱ����У�
��cn=bn+2����{cn}�ǵȱ����У�
��bn+2=cn=3•2n-1��
��bn=3•2n-1-2��
��3���⣺������{bn}�д��ڲ�ͬ������bp��bq��br��p��q��r��N*��ǡ�óɵȲ����У�
������p��q��r����Ȼ{bn}�ǵ������У���2bq=bp+br��12�֣�
��2��3•2q-1-2��=��3•2p-1-2��+��3•2r-1-2��������ã�2•2q-r=2p-r+1��*����14�֣�
����p��q��r��N*����p��q��r��֪q-r��1��p-r��2��
�ࣨ*��ʽ���Ϊż�����ұ�Ϊ������
������{bn}�в����ڲ�ͬ������bp��bq��br��p��q��r��N*��ǡ�óɵȲ����У�
bn+1=a��n+1��1+a��n+1��2+��+a��n+1����n+1��=n+1+��an1+an2��+��+��an��n-1��ann��+n+1=2��an1+an2+��+ann��+2=2bn+2��
��2��֤������bn+1=2bn+2��
��bn+1+2=2��bn+2��
��{bn+2}����b1+2=3Ϊ���2Ϊ���ȵĵȱ����У�
��cn=bn+2����{cn}�ǵȱ����У�
��bn+2=cn=3•2n-1��
��bn=3•2n-1-2��
��3���⣺������{bn}�д��ڲ�ͬ������bp��bq��br��p��q��r��N*��ǡ�óɵȲ����У�
������p��q��r����Ȼ{bn}�ǵ������У���2bq=bp+br��12�֣�
��2��3•2q-1-2��=��3•2p-1-2��+��3•2r-1-2��������ã�2•2q-r=2p-r+1��*����14�֣�
����p��q��r��N*����p��q��r��֪q-r��1��p-r��2��
�ࣨ*��ʽ���Ϊż�����ұ�Ϊ������
������{bn}�в����ڲ�ͬ������bp��bq��br��p��q��r��N*��ǡ�óɵȲ����У�
���������⿼���˵Ȳ����к͵ȱ����еĻ������ʺ����еĵ��ƹ�ʽ��������ѧ���ļ��������Ͷ����е��ۺ����գ�����ʱע������˼���ת��˼������ã������е��⣮

��ϰ��ϵ�д�
�����Ŀ
����P�ں���y=sin2x��ͼ�����ƶ�������Q��x��y������
=��
��0������Q�Ĺ켣����Ϊ��������
| PQ |
| �� |
| 8 |
A��y=sin��2x+
| ||
B��y=sin��2x-
| ||
C��y=sin��2x+
| ||
D��y=sin��2x-
|
 ��֪����P-ABCD������ABCD�ǡ�A=60�㡢�߳�Ϊa�����Σ���PD�͵�ABCD����PD=CD����M��N�ֱ�����AD��PC���е㣮
��֪����P-ABCD������ABCD�ǡ�A=60�㡢�߳�Ϊa�����Σ���PD�͵�ABCD����PD=CD����M��N�ֱ�����AD��PC���е㣮