题目内容
在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且
=
．
（1）确定角C的大小；
（2）若c=
，且△ABC的面积为
，求a+b的值．
| a |
| sinA |
| 2c | ||
|
（1）确定角C的大小；
（2）若c=
| 7 |
3
| ||
| 2 |
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：（1）已知等式左边利用正弦定理化简，求出sinC的值，根据C为锐角，即可确定出C的度数；
（2）由三角形面积公式列出关系式，将c，sinC及已知面积代入求出ab的值，利用余弦定理列出关系式，再利用完全平方公式变形，将ab的值代入求出a+b的值即可．
（2）由三角形面积公式列出关系式，将c，sinC及已知面积代入求出ab的值，利用余弦定理列出关系式，再利用完全平方公式变形，将ab的值代入求出a+b的值即可．
解答：
解：（1）∵
=
，由正弦定理得
=
，
∴
=
，即sinC=
，
∵△ABC是锐角三角形，
∴C=
；
（2）∵c=
，C=
，△ABC的面积为
，
∴
absin
=
，
∴ab=6，
由余弦定理得a2+b2-2abcos
=（a+b）2-3ab=7，
∴（a+b）2=25，
∴a+b=5．
| a |
| sinA |
| 2c | ||
|
| a |
| sinA |
| c |
| sinC |
∴
| 2c | ||
|
| c |
| sinC |
| ||
| 2 |
∵△ABC是锐角三角形，
∴C=
| π |
| 3 |
（2）∵c=
| 7 |
| π |
| 3 |
3
| ||
| 2 |
∴
| 1 |
| 2 |
| π |
| 3 |
3
| ||
| 2 |
∴ab=6，
由余弦定理得a2+b2-2abcos
| π |
| 3 |
∴（a+b）2=25，
∴a+b=5．
点评：此题考查了正弦、余弦定理，以及三角形面积公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
若函数f（x）=x2+ax，x∈R，常数a∈R，则（ ）
| A、存在a，使f（x）是奇函数 |
| B、存在a，使f（x）是偶函数 |
| C、?a∈R，f（x）在（0，+∞）上是增函数 |
| D、?a∈R，f（x）在（-∞，0）上是减函数 |
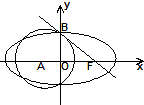如图，已知点F为椭圆C：