题目内容
5．已知抛物线方程为y2=4x，点Q的坐标为（2，3），P为抛物线上动点，则点P到准线的距离与到点Q的距离之和的最小值为$\sqrt{10}$．分析 根据抛物线的定义，点P到点A（2，3）的距离与P到该抛物线准线的距离之和等于点P到点A（2，3）的距离与P到焦点F的距离之和，当且仅当三点A、P、F共线时，点P到点A（2，3）的距离与P到该抛物线准线的距离之和最小．
解答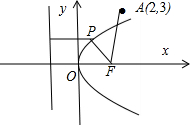 
解：抛物线y2=4x的焦点坐标为（1，0），
根据抛物线的定义，点P到点A（2，3）的距离与P到该抛物线准线的距离之和等于点P到点A（2，3）的距离与P到焦点F的距离之和，
当且仅当三点A、P、F共线时，点P到点A（2，3）的距离与P到该抛物线准线的距离之和最小，
此时，最小值为|AF|=$\sqrt{（2-1）^{2}+（3-0）^{2}}=\sqrt{10}$，
故答案为：$\sqrt{10}$．
点评 本题考查抛物线的定义，考查求距离和，解题的关键是点P到点A（2，3）的距离与P到该抛物线准线的距离之和转化为点P到点A（2，3）的距离与P到焦点F的距离之和，属于中档题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
10．已知角α的终边与单位圆相交于点$P（{{{\frac{4}{5}}_{\;}}，-\frac{3}{5}}）$，现将角α的终边绕坐标原点沿逆时针方向旋转$\frac{π}{3}$，所得射线与单位圆相交于点Q，则点Q的横坐标为（ ）
| A． | $\frac{{4+3\sqrt{3}}}{10}$ | B． | $\frac{{4-3\sqrt{3}}}{10}$ | C． | $\frac{{3+4\sqrt{3}}}{10}$ | D． | $\frac{{4\sqrt{3}-3}}{10}$ |
17．数列{an}满足a1=2，a2=1，并且$\frac{{a}_{n}}{{a}_{n-1}}$+$\frac{{a}_{n}}{{a}_{n+1}}$=2（n≥2），则数列{an}的第100项为（ ）
| A． | $\frac{1}{{{2^{100}}}}$ | B． | $\frac{1}{{{2^{50}}}}$ | C． | $\frac{1}{100}$ | D． | $\frac{1}{50}$ |
15．
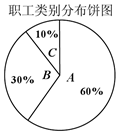某保险公司针对一个拥有20000人的企业推出一款意外险产品，每年每位职工只要交少量保费，发生意外后可一次性获得若干赔偿金．保险公司把企业的所有岗位共分为A、B、C三类工种，从事三类工种的人数分布比例如图，根据历史数据统计出三类工种的赔付频率如下表（并以此估计赔付频率）．
对于A、B、C三类工种职工每人每年保费分别为a元，a元，b元，出险后的赔偿金额分别为100万元，100万元，50万元，保险公司在开展此项业务过程中的固定支出为每年10万元．
（Ⅰ）若保险公司要求利润的期望不低于保费的20%，试确定保费a、b所要满足的条件；
（Ⅱ）现有如下两个方案供企业选择；
方案1：企业不与保险公司合作，企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工；
方案2：企业与保险公司合作，企业负责职工保费的60%，职工个人负责保费的40%，出险后赔偿金由保险公司赔付．
若企业选择方案2的支出（不包括职工支出）低于选择方案1的支出期望，求保费a、b所要满足的条件，并判断企业是否可与保险公司合作．（若企业选择方案2的支出低于选择方案1的支出期望，且与（Ⅰ）中保险公司所提条件不矛盾，则企业可与保险公司合作．）
某保险公司针对一个拥有20000人的企业推出一款意外险产品，每年每位职工只要交少量保费，发生意外后可一次性获得若干赔偿金．保险公司把企业的所有岗位共分为A、B、C三类工种，从事三类工种的人数分布比例如图，根据历史数据统计出三类工种的赔付频率如下表（并以此估计赔付频率）．| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
（Ⅰ）若保险公司要求利润的期望不低于保费的20%，试确定保费a、b所要满足的条件；
（Ⅱ）现有如下两个方案供企业选择；
方案1：企业不与保险公司合作，企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工；
方案2：企业与保险公司合作，企业负责职工保费的60%，职工个人负责保费的40%，出险后赔偿金由保险公司赔付．
若企业选择方案2的支出（不包括职工支出）低于选择方案1的支出期望，求保费a、b所要满足的条件，并判断企业是否可与保险公司合作．（若企业选择方案2的支出低于选择方案1的支出期望，且与（Ⅰ）中保险公司所提条件不矛盾，则企业可与保险公司合作．）