题目内容
19.已知函数f(x)=lnx+x2+x.正实数x1,x2满足f(x1)+f(x2)+x1x2=0,则下述结论中正确的一项是( )| A. | x1+x2≥$\frac{\sqrt{5}-1}{2}$ | B. | x1+x2<$\frac{\sqrt{5}-1}{2}$ | C. | x1+x2≥$\frac{\sqrt{5}+1}{2}$ | D. | x1+x2<$\frac{\sqrt{5}+1}{2}$ |
分析 得到(x1+x2)2+(x1+x2)=x1x2-ln(x1x2),这样令t=x1x2,t>0,容易求得函数t-lnt的最小值为1,从而得到(x1+x2)2+(x1+x2)≥1,解这个关于x1+x2的一元二次不等式即可得出要证的结论.
解答 由f(x1)+f(x2)+x1x2=0,
即lnx1+x12+x1+lnx2+x22+x2+x1x2=0,
从而(x1+x2)2+(x1+x2)=x1x2-ln(x1x2),
令t=x1x2,则由h(t)=t-lnt得,h′(t)=$\frac{t-1}{t}$,
可知,h(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
∴h(t)≥h(1)=1,
∴(x1+x2)2+(x1+x2)≥1,又x1+x2>0,因此x1+x2≥$\frac{\sqrt{5}-1}{2}$成立.
故选:A.
点评 本题考查了函数的单调性问题,考查导数的应用以及换元思想、转化思想,不等式的解法,属于中档题.

练习册系列答案
相关题目
15.已知等差数列{an}的a1=-20,公差为d,前n项和为Sn,则“3<d<5”是“Sn的最小值仅为S6”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,-1),|$\overrightarrow{b}$|=1,且$\overrightarrow{b}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
7.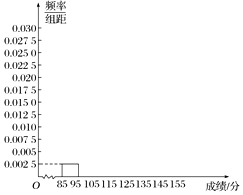 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
(1)表格中①②③④处的数值分别为1、0.025、0.100、1.000;
(2)在图中画出[85,155]的频率分布直方图;
(3)根据题干信息估计总体平均数,并估计总体落在[125,155]上的频率.
 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)在图中画出[85,155]的频率分布直方图;
(3)根据题干信息估计总体平均数,并估计总体落在[125,155]上的频率.
4.定义在R上的函数y=f(x)满足:f(x)+f'(x)>1,f(0)=2018,则不等式exf(x)-ex>2017(其中e为自然对数的底数)的解集为( )
| A. | (2017,+∞) | B. | (-∞,0)∪(2017,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
9.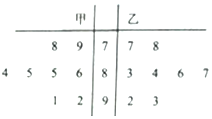 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )| A. | 85,86 | B. | 85,85 | C. | 86,85 | D. | 86,86 |