题目内容
3.已知直线l的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=1+tsinα}\end{array}\right.$(0≤α<π,t为参数),曲线C的极坐标方程为ρ=$\frac{4cosθ}{si{n}^{2}θ}$.(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线l经过点(1,0),求直线l被曲线C截得的线段AB的长.
分析 (Ⅰ)将原极坐标方程ρ=$\frac{4cosθ}{si{n}^{2}θ}$两边同时乘以ρ,利用极坐标与直角坐标之间的关系即可得出其直角坐标方程;
(Ⅱ)将直线l的参数方程化为直角坐标方程,再代入曲线C的标准方程:y2=4x得:x2-6x+1=0,利用直线l经过点(1,0),即可得到直线l被曲线C截得的线段AB的长.
解答 解:(Ⅰ)由ρ=$\frac{4cosθ}{si{n}^{2}θ}$得ρsin2θ=4cosθ得,ρ2sin2θ=4ρcosθ,
即曲线C的直角坐标方程为y2=4x,
故切线C是抛物线;
(Ⅱ)由直线l经过点(1,0)和(0,1),所以其方程为x+y=1.
故直线l的直角坐标方程是x+y-1=0,
联立 $\left\{\begin{array}{l}{x+y-1=0}\\{{y}^{2}=4x}\end{array}\right.$,消去y,得x2-6x+1=0,
则xA+xB=6,
又点(1,0)是抛物线的焦点,
由抛物线定义,得弦长|AB|=xA+xB+2=6+2=8.
点评 本题考查点的极坐标和直角坐标的互化,以及利用平面几何知识解决最值问题.利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
15.已知等差数列{an}的a1=-20,公差为d,前n项和为Sn,则“3<d<5”是“Sn的最小值仅为S6”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.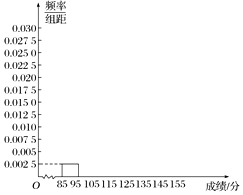 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
(1)表格中①②③④处的数值分别为1、0.025、0.100、1.000;
(2)在图中画出[85,155]的频率分布直方图;
(3)根据题干信息估计总体平均数,并估计总体落在[125,155]上的频率.
 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)在图中画出[85,155]的频率分布直方图;
(3)根据题干信息估计总体平均数,并估计总体落在[125,155]上的频率.
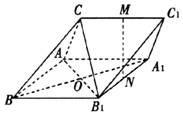 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.