题目内容

2．函数y=$\frac{3x}{x-1}$的值域为{y|y≠3}．

分析 分离常数得到$y=3+\frac{3}{x-1}$，从而可根据$\frac{3}{x-1}≠0$得出y的范围，即得出原函数的值域．

解答 解：$y=\frac{3（x-1）+3}{x-1}=3+\frac{3}{x-1}$；
∵$\frac{3}{x-1}≠0$；
∴y≠3；
∴该函数值域为{y|y≠3}．
故答案为：{y|y≠3}．

点评 考查函数值域的概念及求法，分离常数法的运用，以及反比例函数的值域．

练习册系列答案
相关题目
18．已知f（x）是定义在R上的奇函数，满足f（-$\frac{3}{2}$+x）=f（$\frac{3}{2}$+x），当x∈[0，$\frac{3}{2}$]时，f（x）=ln（x2-x+1），则函数f（x）在区间[0，6]上的零点个数是（　　）
A．3B．5C．7D．9
19．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点分别为A1、A2，上、下顶点分别为B2、B1，四边形A1B1A2B2的面积为4$\sqrt{3}$，且该四边形内切圆的方程为x2+y2=$\frac{12}{7}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）直线l：y=kx+m（k，m均为常数）与椭圆C相交于M，N两个不同的点（M，N异于A1，A2），若以MN为直径的圆过椭圆C的右顶点A2，试判断直线l能否过定点？若能，求出该定点坐标；若不能，也请说明理由．
16．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$=（1，-1），|$\overrightarrow{b}$|=1，且$\overrightarrow{b}$⊥（$\overrightarrow{a}$+$\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）
A．$\frac{π}{4}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{3π}{4}$
3．某学校有若干学生社团，其中“文学社”、“围棋社”、“书法社”的人数分别为9、18、27．现采用分层抽样的方法从这三个社团中抽取6人外出参加活动．
（1）求应从这三个社团中分别抽取的人数；
（2）将抽取的6人进行编号，编号分别为A1，A2，A3，A4，A5，A6，现从这6人中随机地抽出2人组成活动小组．
①用所给编号列出所有可能的结果；
②设A为事件“编号为A1和A2的2人中恰有1人被抽到”，求事件A发生的概率．
7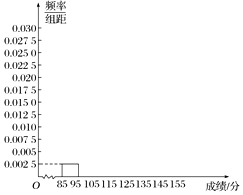．高三年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：
分组频数频率
[85，95）①②
[95，105）0.050
[105，115）0.200
[115，125）120.300
[125，135）0.275
[135，145）4③
[145，155]0.050
合计④
（1）表格中①②③④处的数值分别为1、0.025、0.100、1.000；
（2）在图中画出[85，155]的频率分布直方图；
（3）根据题干信息估计总体平均数，并估计总体落在[125，155]上的频率．
14．在△ABC中，内角A，B，C所对的边分别是a，b，c．已知2a=b+c，sin2A=sinBsinC．试判断三角形的形状．
11．已知函数$f（x）=ln（1+x）-\frac{x}{{{{（1+x）}^a}}}$，实数a＞0．
（Ⅰ）若a=2时，求函数f（x）的单调区间；
（Ⅱ）若x＞0时，不等式f（x）＜0恒成立，求实数a的最大值．
12．复平面上平行四边形ABCD的四个顶点中，A、B、C所对应的复数分别为2-3i、-2-3i、-3+2i，则D点对应的复数是（　　）
A．1+2iB．1-2iC．2-iD．2+i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网