题目内容
已知a、b是异面直线,A、B是a上的两点,C、D是b上的两点,M、N分别是线段AC和BD的中点,则MN和a的位置关系是( )
| A、异面 | B、平行 |
| C、相交 | D、平行、相交或异面 |
考点:空间中直线与平面之间的位置关系
专题:综合题,空间位置关系与距离
分析:利用反证法,判定MN和a只能是异面直线.
解答:
解:若MN和a平行或相交,设它们确定的平面为α,则A、B、M、N均在α内,即AM?α,BN?α.
又C∈AM,D∈BN,
∴C∈α,D∈α,即CD?α,这样直线a、b都在α内,与已知a、b是异面直线矛盾.
故MN和a只能是异面直线.
故选:A.
又C∈AM,D∈BN,
∴C∈α,D∈α,即CD?α,这样直线a、b都在α内,与已知a、b是异面直线矛盾.
故MN和a只能是异面直线.
故选:A.
点评:本题考查空间中直线与平面之间的位置关系,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
利用计算机产生0~1之间的群与随机数a,则事件-
<3a-1<0发生的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}满足a1=0,an+1=an+2n(n∈N*),那么a2011的值是( )
| A、2 0112 |
| B、2 012×2 011 |
| C、2 009×2 010 |
| D、2 010×2 011 |
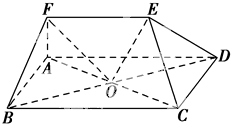 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=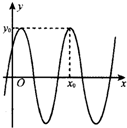 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+