题目内容
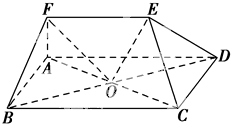 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=| 1 |
| 2 |
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:证法一:要证明FO∥平面CDE,在平面CDE中:取CD中点M,连接OM.证明FO∥EM即可;
证法二:取BC中点G,连接OG,并延长GO交AD于H,连接FH,证明面FGH∥面CDE即可;
证法二:取BC中点G,连接OG,并延长GO交AD于H,连接FH,证明面FGH∥面CDE即可;
解答:
(1)证法一:
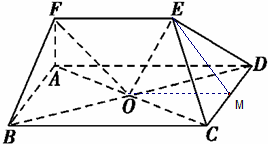
取CD中点M,连接OM,EM,
在矩形ABCD中,OM∥BC且OM=
BC,
又EF∥BC且EF=
BC,则EF∥OM且EF=OM.
所以四边形EFOM为平行四边形,所以FO∥EM.
又因为FO?平面CDE,且EM?平面CDE,
所以FO∥平面CDE.…(12分)
证法二
取BC中点G,连接OG,并延长GO交AD于H,连接FH
在矩形ABCD中,
OG∥CD,
且CD?面CDE,OG?面CDE
OG∥面CDE
又EF∥BC且EF=
BC,则EF∥GC且EF=GC.
所以四边形EFGC为平行四边形,所以FG∥EC.
又因为FG?平面CDE,且EC?平面CDE,
所以FG∥平面CDE.∵FG∩GO=O,FG?面FGH,GO?面FGH∴面FGH∥面CDE,∵OF?面FGH∴OF∥面CDE
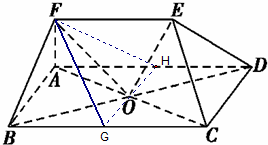

取CD中点M,连接OM,EM,
在矩形ABCD中,OM∥BC且OM=
| 1 |
| 2 |
又EF∥BC且EF=
| 1 |
| 2 |
所以四边形EFOM为平行四边形,所以FO∥EM.
又因为FO?平面CDE,且EM?平面CDE,
所以FO∥平面CDE.…(12分)
证法二
取BC中点G,连接OG,并延长GO交AD于H,连接FH
在矩形ABCD中,
OG∥CD,
且CD?面CDE,OG?面CDE
OG∥面CDE
又EF∥BC且EF=
| 1 |
| 2 |
所以四边形EFGC为平行四边形,所以FG∥EC.
又因为FG?平面CDE,且EC?平面CDE,
所以FG∥平面CDE.∵FG∩GO=O,FG?面FGH,GO?面FGH∴面FGH∥面CDE,∵OF?面FGH∴OF∥面CDE

点评:本题考查直线与平面平行、平面与平面平行等基础知识,考查空间想象能力和推理论证能力.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、若a>b,则ac2>bc2 | ||||
B、若a>b,c<d,则
| ||||
| C、若a>b,c>d,则a-c>b-d | ||||
D、若ab>0,a>b,则
|
已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是( )


| A、7 | ||
B、
| ||
C、
| ||
D、
|
已知a、b是异面直线,A、B是a上的两点,C、D是b上的两点,M、N分别是线段AC和BD的中点,则MN和a的位置关系是( )
| A、异面 | B、平行 |
| C、相交 | D、平行、相交或异面 |
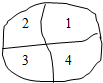 用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有
用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=