题目内容
已知椭圆方程x2+3y2=12,过点D(2,0)的直线l交椭圆于A、B两点,求△OAB面积的最大值.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设直线l的方程为:my=x-2.与椭圆的方程联立可得根与系数的关系,利用弦长公式可得弦弦长|AB|,利用点到直线的距离公式可得原点到直线l的距离,再利用S△OAB=
d|AB|,导数研究函数的单调性极值与最值即可得出.
| 1 |
| 2 |
解答:
解:设直线l的方程为:my=x-2.
联立
,化为(3+m2)y2+4my-8=0.
∴y1+y2=-
,y1y2=
.
∴|AB|=
=
=4
.
点O到直线l的距离d=
.
∴S△OAB=
d|AB|
=
×
×4
=
.
令m2+2=t≥2,
f(t)=t+
,
f′(t)=1-
>0,
∴函数f(t)在[2,+∞)上单调递增,
∴当t=2时,即m=0,f(t)取得最小值
,
∴S△OAB取得最大值
.
∴△OAB面积的最大值是
.
联立
|
∴y1+y2=-
| 4m |
| 3+m2 |
| -8 |
| 3+m2 |
∴|AB|=
| (1+m2)[(y1+y2)2-4y1y2] |
=
(1+m2)[
|
=4
|
点O到直线l的距离d=
| 2 | ||
|
∴S△OAB=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 | ||
|
|
=
2
| ||||
|
令m2+2=t≥2,
f(t)=t+
| 1 |
| t |
f′(t)=1-
| 1 |
| t2 |
∴函数f(t)在[2,+∞)上单调递增,
∴当t=2时,即m=0,f(t)取得最小值
| 5 |
| 2 |
∴S△OAB取得最大值
4
| ||
| 3 |
∴△OAB面积的最大值是
4
| ||
| 3 |
点评:本题考查了直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
•
+
=0,则△ABC为( )
| AB |
| BC |
| AB2 |
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、等腰三角形 |
下列命题中正确的是( )
| A、若a>b,则ac2>bc2 | ||||
B、若a>b,c<d,则
| ||||
| C、若a>b,c>d,则a-c>b-d | ||||
D、若ab>0,a>b,则
|
已知a、b是异面直线,A、B是a上的两点,C、D是b上的两点,M、N分别是线段AC和BD的中点,则MN和a的位置关系是( )
| A、异面 | B、平行 |
| C、相交 | D、平行、相交或异面 |
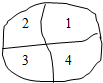 用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有
用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有