题目内容
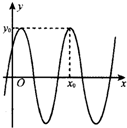 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+| π |
| 6 |
(1)写出f(x)的最小正周期及图中x0、y0的值;
(2)求f(x)在区间[
| π |
| 12 |
| π |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由图象和正弦函数的周期公式可求f(x)的最小正周期及图中x0、y0的值;
(2)先求出2x+
的取值区间,再由正弦函数的单调性即可求出f(x)在区间[
,
]上的最大值和最小值.
(2)先求出2x+
| π |
| 6 |
| π |
| 12 |
| π |
| 2 |
解答:
解:(1)根据图象可知:T=
=π,故比较图象可得x0=
.
y0=3sin(2x0+
)=3sin
=3.
(2)∵x∈[
,
]
∴2x+
∈[
,
π]
又y=sint在[
,
]上单调递增,在[
,
π]上单调递减
∴-
≤sin(2x+
)≤1…(10分)
因此f(x)在[
,
]上的值域为[-
,3]…(12分)
| 2π |
| 2 |
| 7π |
| 6 |
y0=3sin(2x0+
| π |
| 6 |
| 5π |
| 2 |
(2)∵x∈[
| 1 |
| 12 |
| π |
| 2 |
∴2x+
| π |
| 6 |
| π |
| 3 |
| 7 |
| 6 |
又y=sint在[
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 7 |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
因此f(x)在[
| π |
| 12 |
| π |
| 2 |
| 3 |
| 2 |
点评:本题主要考察了正弦函数的图象和性质,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
已知a、b是异面直线,A、B是a上的两点,C、D是b上的两点,M、N分别是线段AC和BD的中点,则MN和a的位置关系是( )
| A、异面 | B、平行 |
| C、相交 | D、平行、相交或异面 |
已知正方体ABCD-A1B1C1D1,E,F是BD上的动点,是AD1上的动点,则( )
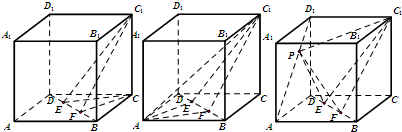

| A、VC-C1EF=VA-C1EF=VP-C1EF |
| B、VC-C1EF=VA-C1EF<VP-C1EF |
| C、VC-C1EF=VA-C1EF>VP-C1EF |
| D、VC-C1EF<VA-C1EF<VP-C1EF |
在平面直角坐标系中,O是坐标原点,已知向量
=(2,a)(a∈R),则“a=-1”是“点M在第四象限”的( )
| OM |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |