题目内容
若定义在R上的函数f(x)满足:
①对任意x,y∈R,都有:f(x+y)=f(x)+f(y)-1;
②当x<0时,f(x)>1.
(Ⅰ)试判断函数f(x)-1的奇偶性;
(Ⅱ)试判断函数f(x)的单调性;
(Ⅲ)若不等式f(a2-2a-7)+
>0的解集为{a|-2<a<4},求f(5)的值.
①对任意x,y∈R,都有:f(x+y)=f(x)+f(y)-1;
②当x<0时,f(x)>1.
(Ⅰ)试判断函数f(x)-1的奇偶性;
(Ⅱ)试判断函数f(x)的单调性;
(Ⅲ)若不等式f(a2-2a-7)+
| 1 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(Ⅰ)令y=-x,f(0)=f(x)+f(-x)-1x=y=0得f(0)=1,再由函数奇偶性的定义验证f(-x)-1与-[f(x)-1]的关系,即可;
(Ⅱ)任取x1,x2∈(-∞,+∞)且x1<x2,求f(x2)-f(x1)的差的符号,有定义法判断出单调性;
(Ⅲ)由题设,将f(a2-2-7)>-
=f(m),再由单调性得出不等式,求出参数,再求函数值.
(Ⅱ)任取x1,x2∈(-∞,+∞)且x1<x2,求f(x2)-f(x1)的差的符号,有定义法判断出单调性;
(Ⅲ)由题设,将f(a2-2-7)>-
| 1 |
| 2 |
解答:
解:(Ⅰ)令y=-x,f(0)=f(x)+f(-x)-1x=y=0得f(0)=1
即f(-x)-1=-[f(x)-1],
∴f(x)-1是奇函数.…(4分)
(Ⅱ)任取x1,x2∈(-∞,+∞)且x1<x2,则f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)+f(x1)-1-f(x1)=f(x2-x1)-1
又x1-x2<0.则f(x1-x2)>1,
∴f(x1-x2)-1>0,
∴f(x2)-f(x1)<0
即:f(x2)<f(x1).
∴f(x)在(-∞,∞)上单调递减.…(9分)
(Ⅲ)f(a2-2-7)>-
=f(m)由(Ⅱ)知:a2-2a-7<m的解集为(-2,4),
∴m=1.即:f(1)=-
.
∴f(2)=-2f(4)=-5f(5)=f(4)+f(1)-1=-
…(14分)
即f(-x)-1=-[f(x)-1],
∴f(x)-1是奇函数.…(4分)
(Ⅱ)任取x1,x2∈(-∞,+∞)且x1<x2,则f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)+f(x1)-1-f(x1)=f(x2-x1)-1
又x1-x2<0.则f(x1-x2)>1,
∴f(x1-x2)-1>0,
∴f(x2)-f(x1)<0
即:f(x2)<f(x1).
∴f(x)在(-∞,∞)上单调递减.…(9分)
(Ⅲ)f(a2-2-7)>-
| 1 |
| 2 |
∴m=1.即:f(1)=-
| 1 |
| 2 |
∴f(2)=-2f(4)=-5f(5)=f(4)+f(1)-1=-
| 13 |
| 2 |
点评:本题考查抽象函数及应用,此类题根据题设与所要解决的问题,对变量进行赋值,是常用的思路.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知a、b是异面直线,A、B是a上的两点,C、D是b上的两点,M、N分别是线段AC和BD的中点,则MN和a的位置关系是( )
| A、异面 | B、平行 |
| C、相交 | D、平行、相交或异面 |
已知向量
=(1,-n),
=(2,n),若
•
=1,则实数n=( )
| a |
| b |
| a |
| b |
| A、1或-1 | B、-1 | C、0 | D、-2 |

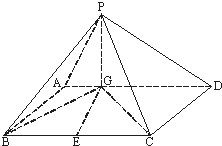 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=